卷积神经网络CNN

前言:依据李沐视频整理

什么是卷积神经网络

卷积神经网络（Convolutional Neural Network，CNN）：是一种前馈神经网络，最早可追溯到1986年的BP算法。

三大网络结构：卷积层（Conv2d）、池化层（MaxPool2d）、全连接层（Linear）
两大特点：稀疏连接、权值共享。可以用更少的参数，获得更高的性能。

全连接层

全连接层（Fully Connected Layers，FC）：torch.nn.Linear(n_hidden, classification_num)

卷积层、池化层、激活函数 —— 将原始数据映射到隐层特征空间，提取特征；

全连接层 —— 将学到的 “分布式特征” 映射到样本标记空间，进行分类

全连接层FC的缺点：

• （1）由于忽略了空间结构，故不适用于目标检测。如：分割任务中的FCN采用卷积层替换全连接层。
• （2）全连接层的参数过多，导致模型复杂度提升，容易过拟合。如：ResNet、GoogleNet采用全局平均池化替换全连接层。

全连接层FC的作用：这一步卷积还有一个非常重要的作用，就是将分布式特征representation映射到样本标记空间。简单来说，就是将输入图像的所有特征整合到一起，输出一个值（猫 / 狗）。
效果：大大减少目标位置的不同，而对分类结果带来的影响。

从全连接到卷积

平移不变性

不管检测对象出现在图像中的哪个位置，神经网络的前面几层应该对相同的图像区域具有相似的反应，即为“平移不变性”。

局部性

只看附近的区域

神经网络的前面几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系，这就是“局部性”原则。最终，可以聚合这些局部特征，以在整个图像级别进行预测。

卷积层

对全连接层使用平移不变性和局部性得到卷积层，卷积层是一个特殊的全连接层

torch.nn.Conv2d(in_channels=3, out_channels=16, kernel_size=5, stride=1, padding=0)

卷积神经网络的核心网络层是卷积层，而卷积层的核心是卷积

卷积运算

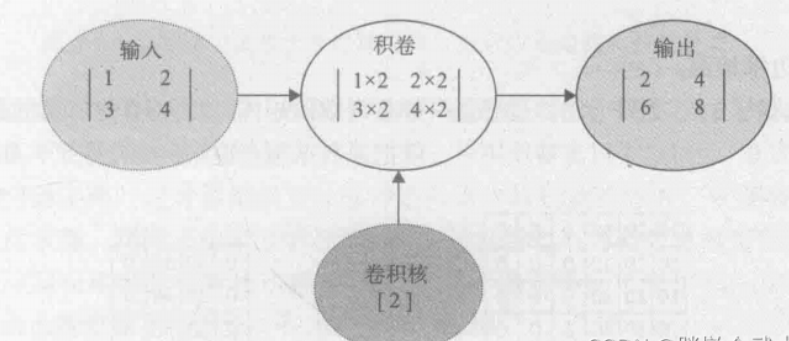
卷积运算公式

$$output = \frac{input - kernel + 2 * padding}{stride} + 1$$

卷积运算的详细过程：

1、取（3 x 3）输入图像中的（2 x 2）矩阵，然后与（2 x 2）卷积核进行卷积运算，得到一个计算结果（ 0 * 0 + 1 * 1 + 3 * 2 + 4 * 3 = 19）；

2、通过滑窗，循环计算得到输出特征图（2 x 2）。

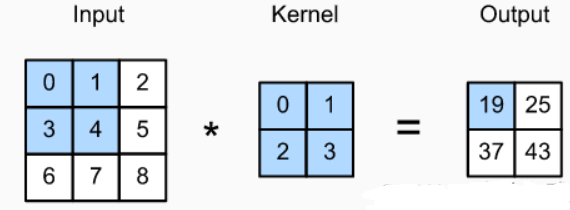
用不同的卷积核能实现不同的效果，如边缘检测，图像锐化，高斯模糊

卷积层将输出和核矩阵进行交叉运算，加上偏移后得到输出

Y = wX + b

w(核矩阵)和b(偏移)是可学习的参数

权值共享

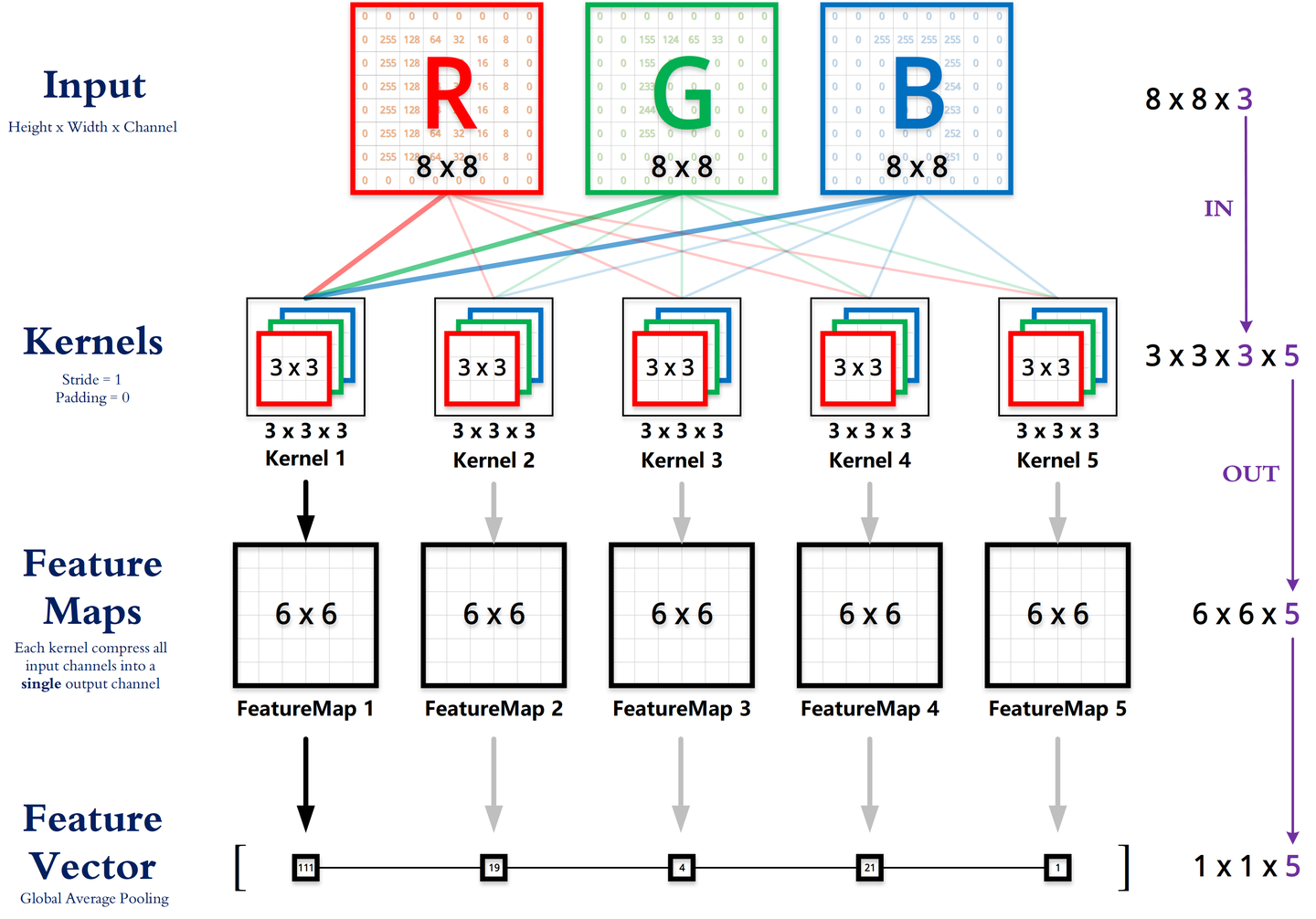
卷积运算（多通道）

1、Kernels卷积核计算
每个 Kernel 的 3 个channle（R/G/B）分别与 Input 对应的 3 个channle（R/G/B）进行卷积运算，最后每个 Kernel 得到 3 个（6 * 6） feature_map_0 。

2、Feature Maps特征图计算
将 3 个（6 * 6）的 feature_map0 逐元素相加（即通道融合）得到 1 个 feature_map_1；
然后将 feature_map1 的每个元素都加上其对应的偏置 b1，得到该 Kernel 的 FeatureMap1。
同一个 Kernel1 对应的 3 个 channle 共享一个偏置 b1（权值共享1）
同一个 FeatureMap1 的所有元素共享一个卷积核 Kernel1（权值共享2）
同理其余Kernel，最后得到（6 * 6 * 5） 个 Feature Maps（即最终输出的 channel 数等于 Kernel 的个数）。

3、Feature Vector向量计算
采用全局最大池化，分别计算每一个Feature Map，最终得到一个（1 * 1 * 5）Feature Vector。

边界填充Padding

图像尺寸对齐，保持边界信息

torch.nn.Conv2d(in_channels=3, out_channels=16, kernel_size=5, stride=1, padding=1)

padding=1：表示在输入图像的边界填充 1 圈，全 0 元素。
作用：

• （1）图像尺寸对齐：对图像进行扩展，扩展区域补零。
• （2）保持边界信息：若没有padding，卷积核将对输入图像的边界像素只卷积一次，而中间像素卷积多次，导致边界信息丢失。

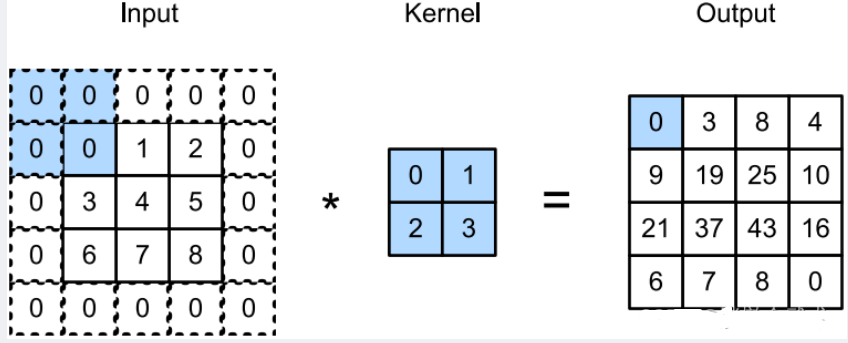
补0圈数的计算公式为：

$$Padding = \frac{kernel - 1}{2}$$

如果想要 con2d 出来的图片长宽没有变化, padding=(kernel_size-1)/2 当 stride=1

stride=1 表示行/列的滑动步长，也就是步幅，是成倍缩小尺寸，而这个参数的值就是缩小的具体倍数，比如步幅为2，输出就是输入的1/2；步幅为3，输出就是输入的1/3

多输入输出通道

多输入通道

每个通道都有一个卷积核，结果是所有通道卷积结果的和，由于输入和卷积核都有ci个通道，我们可以对每个通道输入的二维张量和卷积核的二维张量进行互相关运算，再对通道求和（将ci的结果相加）得到二维张量。这是多通道输入和多输入通道卷积核之间进行二维互相关运算的结果。

多个输出通道

我们可以有多个三位卷积核，每个核生成一个输出通道。用ci和co分别表示输入和输出通道的数目，并让kh和kw为卷积核的高度和宽度。为了获得多个通道的输出，我们可以为每个输出通道创建一个形状为ci×kh×kw的卷积核张量，这样卷积核的形状是co×ci×kh×kw。在互相关运算中，每个输出通道先获取所有输入通道，再以对应该输出通道的卷积核计算出结果。

1x1卷积层

它不识别空间模式，只是融合通道,通常用于调整网络层的通道数量和控制模型复杂性

池化层

通过卷积层获得的图像特征，可以直接训练分类，但很容易导致过拟合。因此需要降采样，增大感受野，防止过拟合。

池化（Pooling）：又叫下采样、降采样。
作用： 降采样（减少参数），增大感受野，提高运算速度及减小噪声影响，防止过拟合。

分类：

• 局部池化
  • 最大池化（Max Pooling）：取Pooling窗口内的最大值作为采样值。
  • 均值池化（Average Pooling）：取Pooling窗口内的所有值相加取均值作为采样值。

torch.nn.MaxPool2d(kernel_size=2, stride=1, padding=0)
torch.nn.AvgPool2d(kernel_size=2, stride=1, padding=0)

• 全局池化
• 全局最大池化（Global Max Pooling）：取以整个特征图为单位的最大值作为采样值。
• 全局均值池化（Global Average Pooling）：取以整个特征图为单位的所有值相加取均值作为采样值。

torch.nn.AdaptiveMaxPool2d(output_size=(2, 2))
torch.nn.AdaptiveAvgPool2d(output_size=(2, 2))

全局池化相比局部池化能减少更多参数，且泛化能力比较好，但唯一的不足之处是收敛速度比较慢。

LeNet

LeNet是早期成功的神经网络。年代久远，这里就只是简单介绍介绍。

架构如图所示

总体来看，LeNet（LeNet-5）由两个部分组成：

• 卷积编码器：由两个卷积层组成;
• 全连接层密集块：由三个全连接层组成。

来看看使用pytorch实现的该模型

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

先使用卷积层来学习图片空间信息，然后使用全连接层来转换到类别空间，在传统的卷积神经网络中，卷积块编码得到的表征在输出之前需由一个或多个全连接层进行处理。