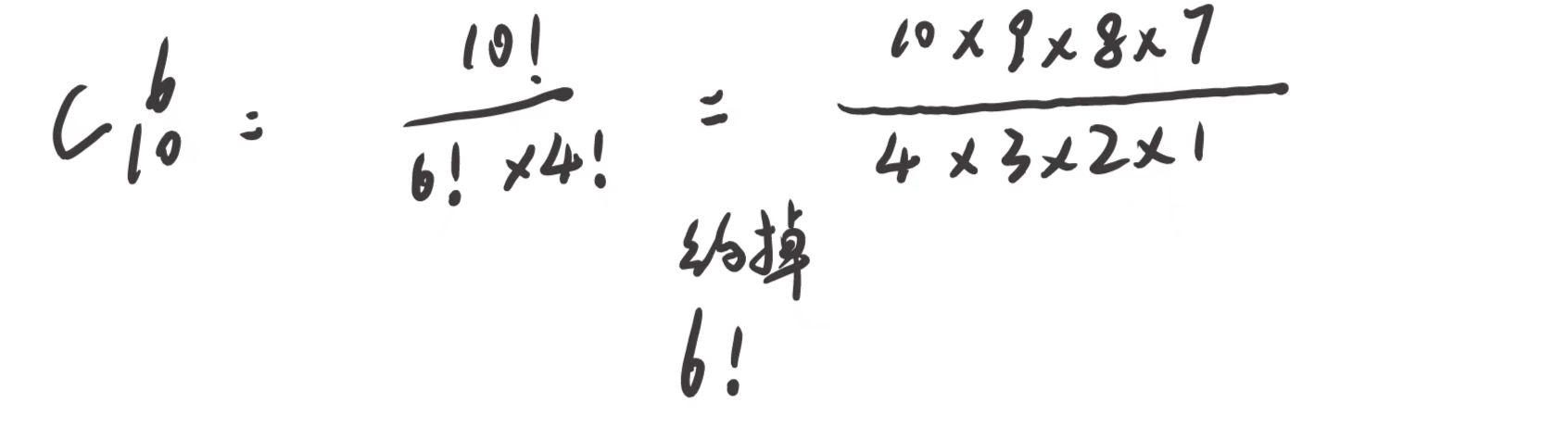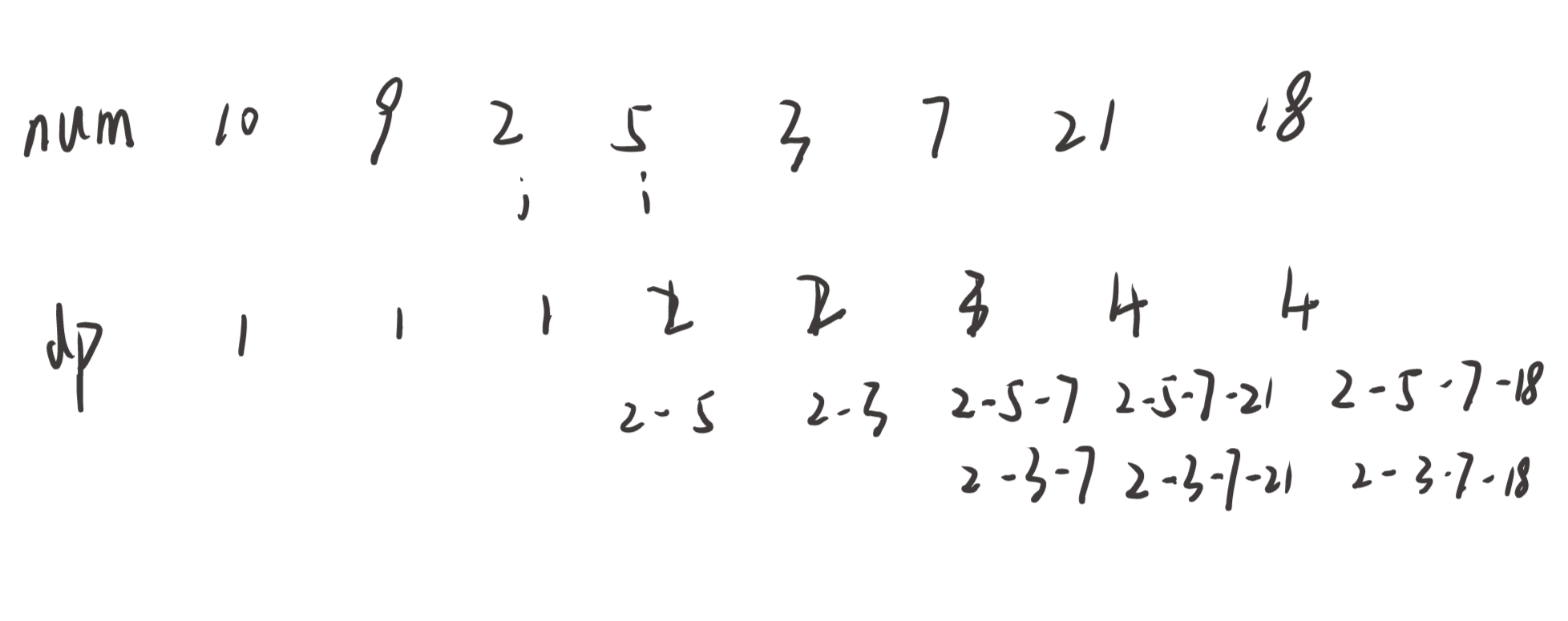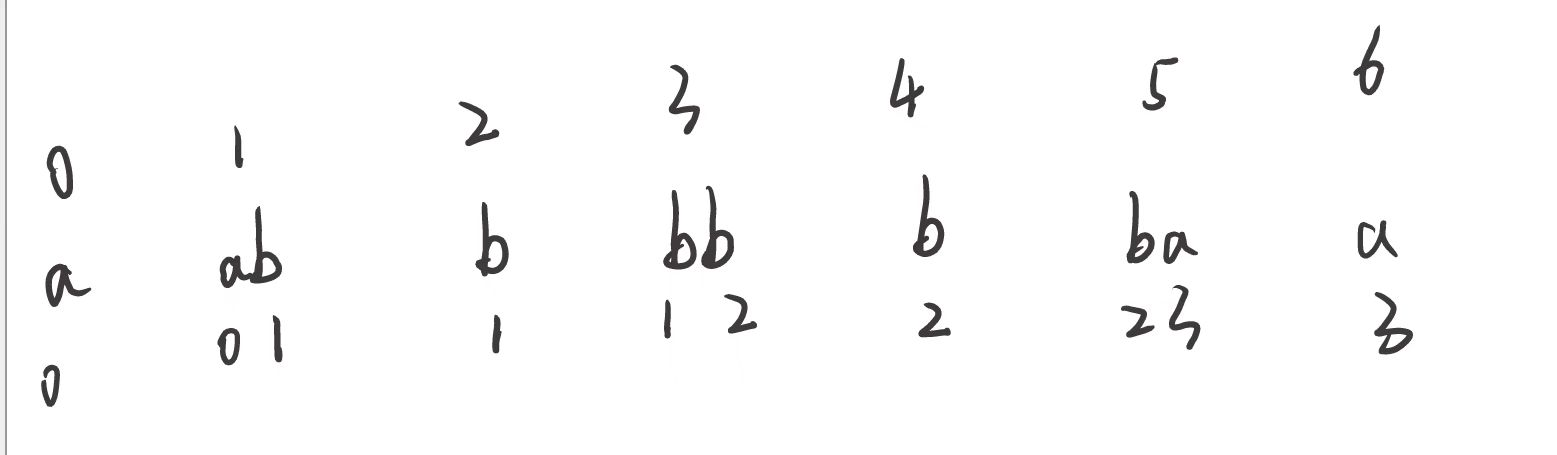leetcodeHot刷题总结

前言

本博客主要是刷leetcode热题100所做的笔记

更新：根据以往的面试经验，给这些题尽量加上输入输出，而不仅仅是函数

输入

public class scan {
    public static void main(String[] args) {
        //输入部分
        Scanner scanner = new Scanner(System.in);

        // 输入一个元素 处理一个
        ArrayList<Integer> list = new ArrayList<>();
        int index = 0;
        while(scanner.hasNextInt()){
            int input = scanner.nextInt();
            list.add(input);
            System.out.print(list.get(index++));
        }
        // 字符串版
        while(scanner.hasNext())
        {
            String string  = scanner.nextLine();
            char [] inputs  = string.toCharArray();
            System.out.println(Arrays.toString(inputs));
        }


        // 输入一行列表的数据  需要加上结束符号
        ArrayList<Integer> list2 = new ArrayList<>();
        System.out.println("开始输入第一个列表的元素，输入'end'结束:");
        while (true) {
            if (scanner.hasNextInt()) {
                int value = scanner.nextInt();
                list2.add(value);
            } else {
                scanner.next(); // 消耗掉非整数的输入
                break;
            }
        }
        System.out.println("输入结束.");
        System.out.println(Arrays.toString(list2.toArray()));


        // 输入字符串转为数组
        ArrayList<Integer> list3 = new ArrayList<>();

        String input1 = scanner.nextLine();
        String[] elements = input1.split("\\s+"); //按照空白
        for (String element : elements) {
            list3.add(Integer.parseInt(element));
        }
        System.out.println(Arrays.toString(list3.toArray()));

        scanner.close();

    }
}

next和nextLine

next()查找并返回来自此扫描器的下一个完整标记。完整标记的前后是与分隔模式匹配的输入信息，所以next方法不能得到带空格的字符串。

nextLine()方法的结束符只是Enter键，即nextLine()方法返回的是Enter键之前的所有字符，它是可以得到带空格的字符串的。

注意点（易错点）： 注意next()方法和nextLine()方法的连用

public class NextTest{  
    public static void main(String[] args) {  
        Scanner input = new Scanner(System.in);  
        System.out.print("请输入第一个字符串：");  
        String s1 = input.next();  
        System.out.print("请输入第二个字符串：");  
        String s2 = input.nextLine();  
        System.out.println("输入的字符串是："+ s1 + " " + s2);  
    }  
} 
//运行结果是：
//请输入第一个字符串：home
//请输入第二个字符串：输入的字符串是：home

可以看到，nextLine()自动读取了被next()去掉的Enter作为它的结束符，所以没办法给s2从键盘输入值。经过验证，发现其他的next的方法，如nextDouble() ，nextFloat() ，nextInt() 等与nextLine()连用时都存在这个问题，解决的办法是：在每一个 next()、nextDouble() 、 nextFloat()、nextInt() 等语句之后加一个nextLine()语句，将被next()去掉的Enter等结束符过滤掉。

//更正为
public class NextTest{  
    public static void main(String[] args) {  
        Scanner input = new Scanner(System.in);  
        System.out.print("请输入第一个字符串：");  
        String s1 = input.next(); 
        input.nextLine();  //接收结束符
        System.out.print("请输入第二个字符串：");  
        String s2 = input.nextLine();  
        System.out.println("输入的字符串是："+ s1 + " " + s2);  
    }  
} 

//在Java代码String word = scanner.nextLine().trim();中，trim()的作用是去除用户输入字符串的前后空白字符
String word = scanner.nextLine().trim();

各种排序算法

package hot100;

import java.util.*;
/**
 * @program: code
 * @description:
 * @author: Mr.Mercury
 * @create: 2025-04-02 13:31
 **/

public class SortingAlgorithms {

    // 1. 冒泡排序
    public static void bubbleSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n-1; i++) {
            boolean swapped = false;
            for (int j = 0; j < n-i-1; j++) {
                if (arr[j] > arr[j+1]) {
                    // 交换相邻元素
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                    swapped = true;
                }
            }
            // 如果没有交换则提前结束
            if (!swapped) break;
        }
    }

    // 2. 选择排序
    public static void selectionSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n-1; i++) {
            int minIndex = i;
            for (int j = i+1; j < n; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            // 将最小值交换到当前位置
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
    }

    // 3. 插入排序
    public static void insertionSort(int[] arr) {
        int n = arr.length;
        for (int i = 1; i < n; i++) {
            int key = arr[i];
            int j = i-1;
            // 将大于key的元素后移
            while (j >= 0 && arr[j] > key) {
                arr[j+1] = arr[j];
                j--;
            }
            arr[j+1] = key;
        }
    }

    // 4. 希尔排序
    public static void shellSort(int[] arr) {
        int n = arr.length;
        // 使用希尔增量序列
        for (int gap = n/2; gap > 0; gap /= 2) {
            for (int i = gap; i < n; i++) {
                int temp = arr[i];
                int j;
                for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
                    arr[j] = arr[j - gap];
                }
                arr[j] = temp;
            }
        }
    }

    // 5. 归并排序
    public static void mergeSort(int[] arr) {
        mergeSort(arr, 0, arr.length-1);
    }

    private static void mergeSort(int[] arr, int left, int right) {
        if (left < right) {
            int mid = left + (right - left)/2;
            mergeSort(arr, left, mid);
            mergeSort(arr, mid+1, right);
            merge(arr, left, mid, right);
        }
    }

    private static void merge(int[] arr, int left, int mid, int right) {
        int[] temp = new int[right - left + 1];
        int i = left, j = mid+1, k = 0;

        while (i <= mid && j <= right) {
            temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
        }
        //拷贝剩余的元素
        while (i <= mid) temp[k++] = arr[i++];
        while (j <= right) temp[k++] = arr[j++];

        System.arraycopy(temp, 0, arr, left, temp.length);
    }

    // 6. 快速排序
    public static void quickSort(int[] arr) {
        quickSort(arr, 0, arr.length-1);
    }

    private static void quickSort(int[] arr, int low, int high) {
        if (low < high) {
            int pi = partition(arr, low, high);
            quickSort(arr, low, pi-1);
            quickSort(arr, pi+1, high);
        }
    }

    private static int partition(int[] arr, int low, int high) {
        int pivot = arr[high]; // 选择最后一个元素为基准
        int i = low - 1;
        for (int j = low; j < high; j++) {
            if (arr[j] < pivot) {
                i++;
                swap(arr, i, j);
            }
        }
        swap(arr, i+1, high);
        return i+1;
    }

    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    // 7. 堆排序
    public static void heapSort(int[] arr) {
        int n = arr.length;
        // 构建最大堆
        for (int i = n/2 -1; i >= 0; i--) {
            heapify(arr, n, i);
        }
        // 逐个提取元素
        for (int i = n-1; i > 0; i--) {
            swap(arr, 0, i);
            heapify(arr, i, 0);
        }
    }

    private static void heapify(int[] arr, int n, int i) {
        int largest = i;
        int left = 2*i + 1;
        int right = 2*i + 2;

        if (left < n && arr[left] > arr[largest]) largest = left;
        if (right < n && arr[right] > arr[largest]) largest = right;

        if (largest != i) {
            swap(arr, i, largest);
            heapify(arr, n, largest);
        }
    }

    // 8. 计数排序（适用于非负整数）
    public static void countingSort(int[] arr) {
        int max = Arrays.stream(arr).max().getAsInt();
        int[] count = new int[max+1];

        for (int num : arr) count[num]++;

        int index = 0;
        for (int i = 0; i <= max; i++) {
            while (count[i]-- > 0) {
                arr[index++] = i;
            }
        }
    }

    // 9. 桶排序（假设输入在[0,1)范围内）
    public static void bucketSort(int[] arr) {
        int n = arr.length;

        // 归一化数组元素到 [0, 1) 范围
        int max = Arrays.stream(arr).max().getAsInt();
        double[] normalizedArr = new double[n];
        for (int i = 0; i < n; i++) {
            normalizedArr[i] = (double) arr[i] / (max + 1);
        }

        // 初始化桶
        ArrayList<Double>[] buckets = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            buckets[i] = new ArrayList<>();
        }

        // 将元素分配到桶中
        for (double num : normalizedArr) {
            int bucketIndex = (int)(num * n);
            buckets[bucketIndex].add(num);
        }

        // 对每个桶排序并合并回原数组
        int index = 0;
        for (ArrayList<Double> bucket : buckets) {
            Collections.sort(bucket);
            for (double num : bucket) {
                arr[index++] = (int) (num * (max + 1)); // 恢复原始值
            }
        }
    }


    // 10. 基数排序（LSD实现）
    public static void radixSort(int[] arr) {
        int max = Arrays.stream(arr).max().getAsInt();
        for (int exp = 1; max/exp > 0; exp *= 10) {
            countingSortByDigit(arr, exp);
        }
    }

    private static void countingSortByDigit(int[] arr, int exp) {
        int n = arr.length;
        int[] output = new int[n];
        int[] count = new int[10];

        for (int num : arr) count[(num/exp)%10]++;

        for (int i = 1; i < 10; i++) count[i] += count[i-1];

        for (int i = n-1; i >= 0; i--) {
            output[count[(arr[i]/exp)%10]-1] = arr[i];
            count[(arr[i]/exp)%10]--;
        }

        System.arraycopy(output, 0, arr, 0, n);
    }

    public static void main(String[] args) {
        // 测试示例
        int[] arr = {64, 34, 25, 12, 22, 11, 90};
        System.out.println("原数组: " + Arrays.toString(arr));

        // 调用不同的排序方法测试
//        bubbleSort(arr);
//        selectionSort(arr);
//        insertionSort(arr);
//        shellSort(arr);
//        mergeSort(arr);
//        quickSort(arr);
//        heapSort(arr);
//        countingSort(arr);
        bucketSort(arr);
//        radixSort(arr);
        System.out.println("桶排序后: " + Arrays.toString(arr));
    }
}

链表

打印链表

剑指 Offer 06. 从尾到头打印链表 - 力扣（Leetcode）

从尾巴到头部打印链表的节点

下面是自己写的垃圾代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public int[] reversePrint(ListNode head) {
        List<Integer> list = new ArrayList<>();
        while(head != null){
            list.add(head.val);
            head = head.next;
        }
      
        int[] res = new int[list.size()];
        int count = 0;
        for(int i = list.size() - 1; i >= 0;i--){
            res[i] = list.get(count++);
        }
        return res;
    }
}

使用递归,将添加进集合这一步骤放到递归的后面，这样后面返回的时候就可以逆序返回了

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    List<Integer> list = new ArrayList<>();
    public int[] reversePrint(ListNode head) {
        dfs(head);
        int[] res = new int[list.size()];
        for(int i = 0; i < list.size(); i++){
            res[i] = list.get(i);
        }
        return res;
      
    }
    void dfs(ListNode node){
            if(node == null){
                return ;
            }
            dfs(node.next);
            list.add(node.val);
        }
}

使用辅助栈来解决

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    
    public int[] reversePrint(ListNode head) {
        Stack<Integer> stack = new Stack<>();
        while(head != null){
            stack.push(head.val);
            head = head.next;
        }
        int[] res = new int[stack.size()];
        for(int i = 0;i < res.length; i++){//这里不能使用stack.size()，因为每次循环后stack的大小都在逐渐变小
            res[i] = stack.pop();
        }
        return res;
    }
    
}

预设pre

使用双指针进行遍历，对于链表问题，返回结果为头结点时，通常需要先初始化一个预先指针 pre，该指针的下一个节点指向真正的头结点head。使用预先指针的目的在于链表初始化时无可用节点值，而且链表构造过程需要指针(cur)移动，进而会导致头指针丢失，无法返回结果。2. 两数相加 - 力扣（LeetCode）

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode temp1,temp2;
        ListNode pre = new ListNode(0);
        ListNode cur = pre;
        temp1 = l1;
        temp2 = l2;
        int carry = 0;
        //这里的carry!=0的判断主要是防止后面还有进位
		while(temp1!=null||temp2!=null||carry!=0){
            int x = temp1 == null ? 0:temp1.val;
            int y = temp2 == null ? 0:temp2.val;
            int resval = x + y + carry;
           
            carry = resval/10;// 刷新carry
            resval = resval % 10;
            
            ListNode body =  new ListNode(resval);
            cur.next = body;
            cur = body;//移动指针

            if(temp1!=null){
                temp1 = temp1.next;
            }
            if(temp2!=null){
                temp2 = temp2.next;
            }
        }
        return pre.next;
    }
}
--------------------------------------------------------------------------------
//have main
    
//手动扫描输入
import java.util.ArrayList;
import java.util.Scanner;

// 定义链表节点
class ListNode {
    int val;
    ListNode next;
    ListNode() {}
    ListNode(int val) { this.val = val; }
    ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}

public class addtwonumbers {
    public static ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode dummyHead = new ListNode(0);
        ListNode current = dummyHead;
        int carry = 0; // 进位标志

        while (l1 != null || l2 != null || carry != 0) {
            int val1 = (l1 != null) ? l1.val : 0;
            int val2 = (l2 != null) ? l2.val : 0;
            int sum = val1 + val2 + carry;
            carry = sum / 10; // 计算是否需要进位
            current.next = new ListNode(sum % 10); // 新节点保存当前位的结果
            current = current.next;

            if (l1 != null) l1 = l1.next;
            if (l2 != null) l2 = l2.next;
        }

        return dummyHead.next;
    }

    public static ListNode buildList(ArrayList<Integer> list, int index) {
        // 如果已经处理完所有的元素，则返回null
        if (index >= list.size()) {
            return null;
        }
        // 创建一个新的节点，并且递归地为下一个节点调用此方法
        ListNode node = new ListNode(list.get(index), buildList(list, index + 1));
        return node;
    }

    // 测试函数
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        ArrayList<Integer> list1 = new ArrayList<>();
        ArrayList<Integer> list2 = new ArrayList<>();

        String input1 = scanner.nextLine();
        String[] elements1 = input1.split("\\s+");
        for (String element : elements1) {
            list1.add(Integer.parseInt(element));
        }

        String input2 = scanner.nextLine();
        String[] elements2 = input2.split("\\s+");
        for (String element : elements2) {
            list2.add(Integer.parseInt(element));
        }

        scanner.close();

        ListNode l1 = buildList(list1, 0);
        ListNode l2 = buildList(list2, 0);
        ListNode result = addTwoNumbers(l1, l2);

        // 打印结果
        while (result != null) {
            System.out.print(result.val + " ");
            result = result.next;
        }
    }
}

//直接初始化的主函数
public static void main(String[] args) {
    Solution solution = new Solution();
    ListNode l1 = new ListNode(2, new ListNode(4, new ListNode(3)));
    ListNode l2 = new ListNode(5, new ListNode(6, new ListNode(4)));
    ListNode result = solution.addTwoNumbers(l1, l2);

    // 打印结果
    while (result != null) {
        System.out.print(result.val + " ");
        result = result.next;
    }
}

常用的经典代码

熟记单链表经典的删除，获取有效节点，查找倒数第几个(也可以使用快慢指针)，有时也需要考虑到特殊情况，比如删除的节点就是头节点，就找不到待删除的前一个节点，需要单独判断(预设一个pre节点的话就不需要，这就是预设节点的好处)，比如19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode）,这个题解看下面的删除节点

//删除
cur.next = cur.next.next; 


//查找倒数第几个一般是 总长减去倒数
for(int i =0; i< size - index; i++) {
	cur = cur.next;
}


//获取链表的有效节点数
public static int getLength(ListNode head) {
  if(head.next == null) { //带头结点的空链表，不带头节点的删除就好
    return 0;
  }
  int length = 0;

  HeroNode cur = head.next;
  while(cur != null) {
    length++;
    cur = cur.next; //遍历写一个
  }
  return length;
}

翻转链表

剑指 Offer 24. 反转链表 - 力扣（Leetcode）

采用迭代的方式来实现翻转这个链表

//翻转链表
    public ListNode reverseList(ListNode head) {
        ListNode cur = head;
        ListNode pre = null;//存储已经翻转链表的头节点
        while(cur != null){
            ListNode temp = cur.next;//先把后面的节点保存起来防止断裂
            cur.next = pre;//将已经翻转的链表的头节点接上去
            pre = cur;
            cur = temp;//后移
        }
        return pre;
    }

头插法

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        //采用头插法翻转
        ListNode pre = new ListNode(0);
        ListNode cur = head;
        while(cur != null){
            ListNode temp = cur.next;
            cur.next = pre.next;
            pre.next = cur;
            cur = temp;
        }
        return pre.next;
    }
}

92. 反转链表 II - 力扣（LeetCode）

反转一个指定区间里面的链表节点

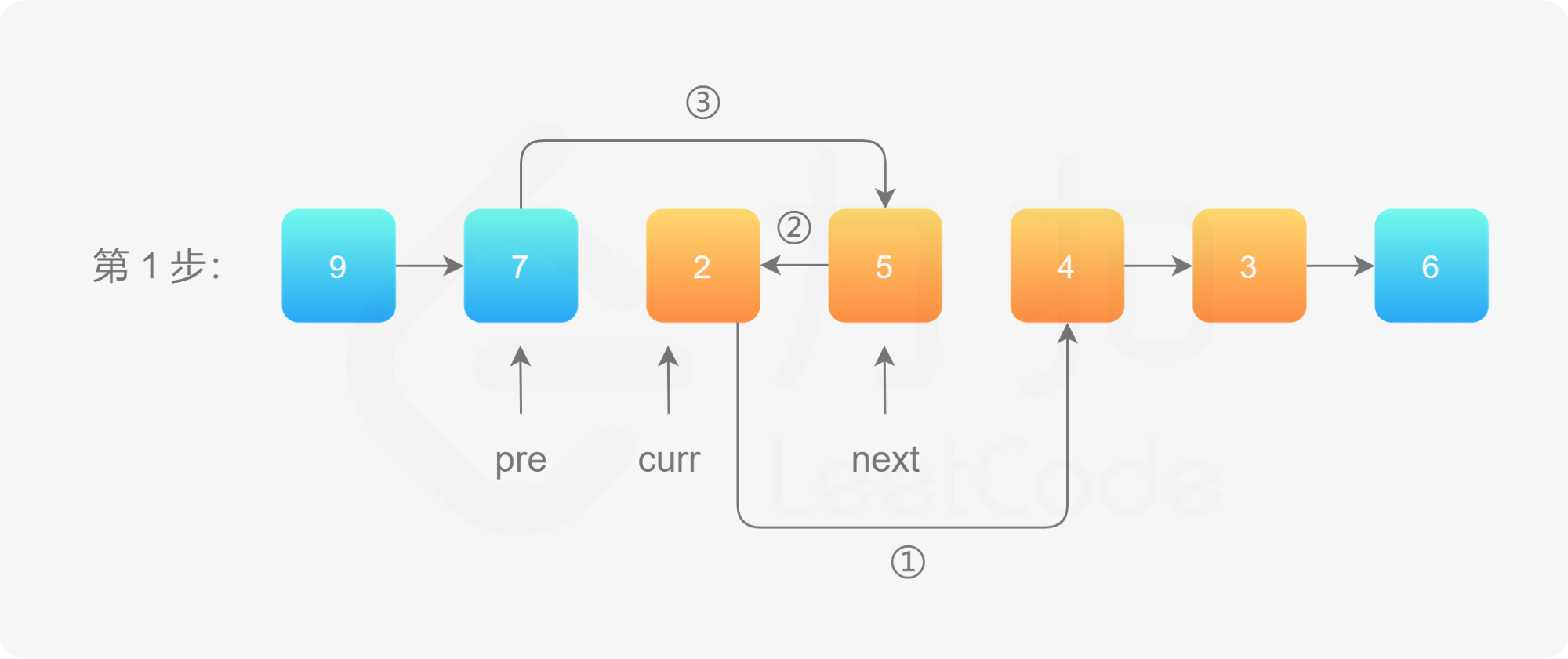
使用三个链表的变量来记录在翻转的时候需要的指针变量，分别是pre,cur,next

curr：指向待反转区域的第一个节点 left；
next：永远指向 curr 的下一个节点，循环过程中，curr 变化以后 next 会变化；
pre：永远指向待反转区域的第一个节点 left 的前一个节点，在循环过程中不变。

第一步 图示

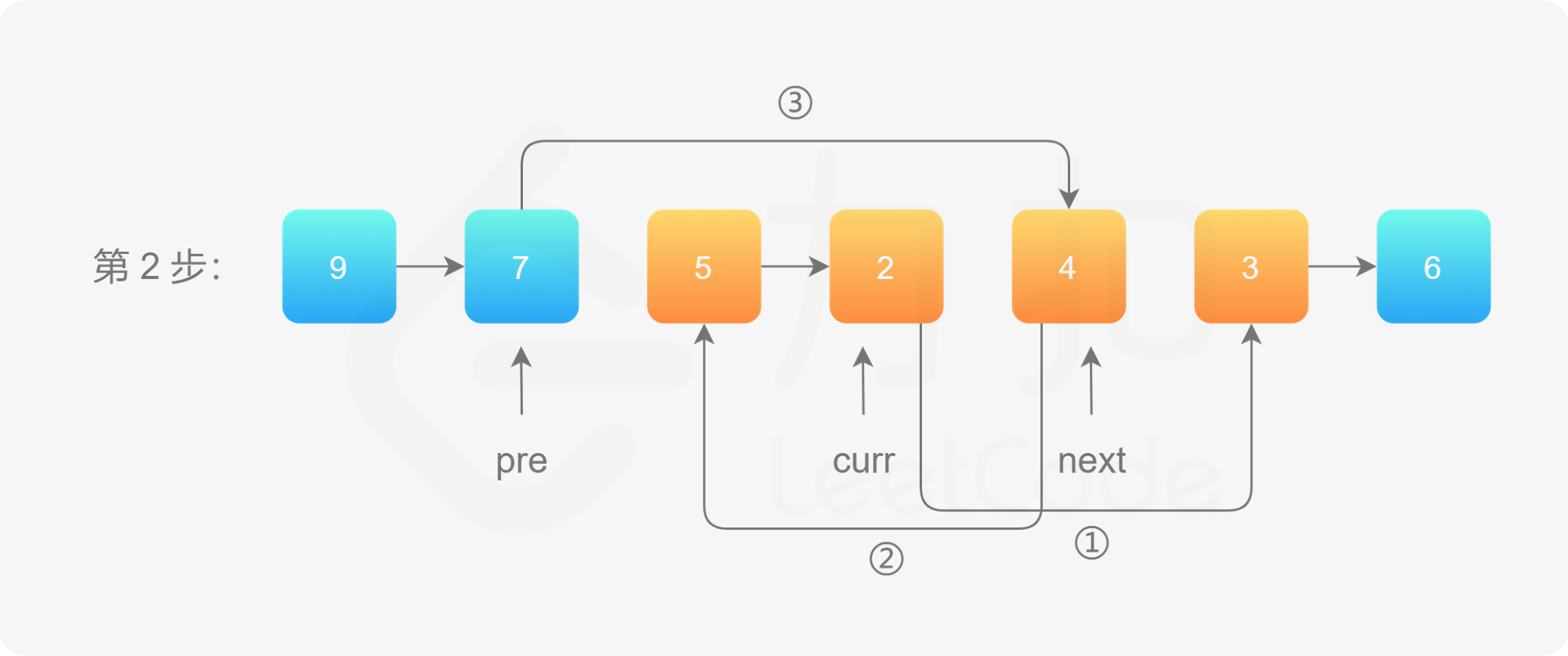
/第二步 图示

class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        // 设置 dummyNode 是这一类问题的一般做法
        ListNode dummyNode = new ListNode(-1);
        dummyNode.next = head;
        ListNode pre = dummyNode;
        for (int i = 0; i < left - 1; i++) {
            pre = pre.next;
        }
        ListNode cur = pre.next;
        ListNode next;
        for (int i = 0; i < right - left; i++) {
            next = cur.next;
            cur.next = next.next;
            next.next = pre.next;
            pre.next = next;
        }
        return dummyNode.next;
    }
}

删除节点

剑指 Offer 18. 删除链表的节点 - 力扣（Leetcode） 之前自己写的代码，老是报空指针异常。。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode deleteNode(ListNode head, int val) {
        ListNode pre = new ListNode(-1);
        pre.next = head;

        ListNode cur = pre;
        //找到前一个节点
        while(cur.next != null && cur.next.val != val){
            cur = cur.next;
        }
        //删除节点
        cur.next = cur.next.next;
        return pre.next;
    }
}

19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode）

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        int length  = getlength(head);
        //添加一个pre，这样删除到头节点时不会出现空指针异常
        ListNode pre = new ListNode();
        pre.next = head;
        ListNode cur = pre;
        //寻找倒数第几个进行删除，需要找到前一个进行操作
        for(int i = 0;i < length - n;i++){
            cur = cur.next;
        }
        //进行删除
        cur.next = cur.next.next;
        return pre.next;
    }

    public int getlength(ListNode head){
        ListNode cur = head;
        int length = 0;
        while(cur != null){
            length++;
            cur = cur.next;
        }
        return length;
    }
}


//have main
public class removeNthFromEnd {
    public static ListNode buildList(ArrayList<Integer> list, int index) {
        // 如果已经处理完所有的元素，则返回null
        if (index >= list.size()) {
            return null;
        }
        // 创建一个新的节点，并且递归地为下一个节点调用此方法
        ListNode node = new ListNode(list.get(index), buildList(list, index + 1));
        return node;
    }
    public static ListNode removeNthFromEnd(ListNode head, int n) {
        int length  = getlength(head);

        ListNode pre = new ListNode();
        pre.next = head;
        ListNode cur = pre;
        //寻找倒数第几个进行删除，需要找到前一个进行操作
        for(int i = 0;i < length - n;i++){
            cur = cur.next;
        }
        //进行删除
        cur.next = cur.next.next;
        return pre.next;
    }

    public static int getlength(ListNode head){
        ListNode cur = head;
        int length = 0;
        while(cur != null){
            length++;
            cur = cur.next;
        }
        return length;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        ArrayList<Integer> list = new ArrayList<>();
        for(int i = 0;i < n;i++) {
            list.add(scanner.nextInt());
        }
        ListNode listNode = buildList(list,0);

        //删除倒数第几个
        int target = scanner.nextInt();
        listNode = removeNthFromEnd(listNode,target);
        while (listNode != null){
            System.out.print(listNode.val + " ");
            listNode = listNode.next;
        }
    }
}

快慢指针

判断链表是否有环，并找出环的入口

比如141. 环形链表 - 力扣（LeetCode）和142. 环形链表 II - 力扣（LeetCode）就是这种题

如果链表存在环，就好像操场的跑道是一个环形一样。此时让快慢指针都从链表头开始遍历，快指针每次向前移动两个位置，慢指针每次向前移动一个位置；如果快指针到达NULL，说明链表以NULL为结尾，没有环。如果快指针追上慢指针，则表示有环。

​ 如果链表存在环，如果找到环的入口点？当fast若与slow相遇时，slow肯定没有走遍历完链表或者恰好遍历一圈。于是我们从链表头与相遇点分别设一个指针，每次各走一步，两个指针必定相遇，且相遇第一点为环入口点(证明略)。

public boolean hasCirle(ListNode head){
    if(head == null){//考虑只有一个节点的特殊情况
        return false;
    }
    ListNode slow = head,fast = head;
    while(fast != null && fast.next != null){//这里一起写上fast.next判断可以避免空指针异常
        slow = slow.next; //每次前进一步
        fast = fast.next.next; //每次前进两步
        if(slow == fast){
            return true;
        }
    }
    return false;
}

public ListNode findLoopPort(ListNode head){
        ListNode slow = head,fast = head;
        if(head == null){
            return null;
        }
        while(true){
            if(fast == null || fast.next == null){
                return null;
            }
            fast = fast.next.next;
            slow = slow.next;//放在if的外面，防止第一次的时候判断失误
            if( slow == fast){
                break;
            }
        }
        slow = head;//让slow返回
        while(slow != fast){
            fast = fast.next;
            slow = slow.next;//之后就是每次移动一步
        }
        //再次相遇的时候就是环开始的节点
        return slow;
}

这里可以再加一道题287. 寻找重复数 - 力扣（Leetcode）

题意：在那个数组里面，只有一个数字会出现一次或者多次，其他数字只会出现一次，找出这个数

思路：这道题一看到，我就想到了哈希映射，做了一遍，思路是对的，也可以通过

class Solution {
    public int findDuplicate(int[] nums) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int i = 0;i < nums.length;i++){
            //找出这个数字的映射出现了几次
            int count  = map.get(nums[i]) == null ? 1 : map.get(nums[i]) + 1;
            map.put(nums[i],count);
        }
        //找出不是1的映射就是答案
        for(int i = 0;i<nums.length;i++){
            if(map.get(nums[i]) != 1){
                return nums[i];
            }
        }
        return -1;
    }
}

题解一位大佬给出了另外一种快慢指针的思路，可以将这道题通过下标相互"连接",将题目转换为环形链表的思路，通过找出入口的方式，就可以找出这个重复的值287. 寻找重复数题解

class Solution {
    public int findDuplicate(int[] nums) {
        int slow = 0;
        int fast = 0;
        slow = nums[slow];
        fast = nums[nums[fast]];
        while(slow != fast){
            slow = nums[slow];
            fast = nums[nums[fast]];
        }
        int pre1 = 0;
        int pre2 = slow;
        while(pre1 != pre2){
            pre1 = nums[pre1];
            pre2 = nums[pre2];
        }
        return pre1;
    }
}

在有序链表中寻找中位数

快指针的移动速度是慢指针的2倍，因此当快指针到达链表尾的时候，满指针到达中点。

程序还要考虑链表结点个数的奇偶数因素，当快指针移动x次后到达表尾（1+2x），说明链表有奇数个结点，直接返回慢指针指向的数据即可。

如果快指针是倒数第二个结点，说明链表结点个数是偶数，这时可以根据“规则”返回上中位数或下中位数或（上中位数+下中位数）的一半。

private ListNode middleNode(ListNode head) {
    while(fast && slow){
        if(fast.next == null){//奇数
            return slow;
        }else if(fast.next != null && fast.next.next == null){//偶数 注意这个判断条件 和之前不一样 是多了一个next
            return slow; //这里的slow是中点的前一个
        }else{
            fast = fast.next.next;
            slow = slow.next;
        }
    }
}

输出链表中的倒数第K个节点

快指针先向前走K下，慢指针不动，之后，快慢指针一起动，当快指针到达尾节点的时候，慢指针就是倒数第k个节点

ListNode fast = pre, slow = pre;
while(n != 0) {
    fast = fast.next;
    n--;
}
while(fast.next != null) {
    fast = fast.next;
    slow = slow.next;
}

例题：剑指 Offer 22. 链表中倒数第k个节点 - 力扣（Leetcode）

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode getKthFromEnd(ListNode head, int k) {
        ListNode fast = head;
        ListNode slow = head;
        while(fast != null && k > 0){
            fast = fast.next;
            k--;
        }
        while(fast != null){
            fast = fast.next;
            slow = slow.next;
        }
        return slow;
    }
}

快慢指针和翻转链表一起

234. 回文链表 - 力扣（LeetCode）该题就是叫你判断一个链表里面的数据是否是回文，用以前取余相乘翻转判断显然不行，因此这里可以考虑使用使用快慢指针寻找中点，并结合翻转链表，将前半段链表翻转，以此来比较，但是下面所示的该方法没有将链表翻转回来，具有一定的缺陷。

public boolean isPalindrome(ListNode head) {
        ListNode slow = head,fast = head;
        ListNode pre = null;//用来存储已经翻转节点前驱
        while(fast != null && fast.next != null){//快慢指针经典语法
            fast = fast.next.next;
            //注意！！！ 
            //这里需要写在最前面，不然都话，先翻转链表断裂后，fast指针无法走过去，会出现空指针异常
            ListNode temp = slow.next;//用来暂时存储后续节点，防止断裂
            slow.next = pre;//翻转，将前面所有已翻转节点接到slow后面
            pre = slow;//记录位置
            slow = temp;//相当于后移了slow指针
        }
        if(fast != null){//链表节点数是单数
             slow = slow.next;//slow移动到中间节点的另一边去，好和前面已经翻转的节点进行比较
        }
        while(slow != null){//开始比较
            if(slow.val != pre.val){
                return false;//结果不相等
            }
            slow = slow.next;
            pre = pre.next;
        }
        return true;
    }

第二种解法

使用集合存储数据之后，使用双指针从两边开始比较，但是效率没有上面的高，代码如下

public boolean isPalindrome(ListNode head) {
        ArrayList<Integer> data = new ArrayList<>();
        ListNode temp = head;
        while(temp != null){
            data.add(temp.val);
            temp = temp.next; //将数据全部遍历后加入集合
        }
        int start = 0;
        int end = data.size() - 1;
        while(start < end){
            if(data.get(start) != data.get(end)){
               return false; 
            }
            start++;
            end--;
        }
        return true;
    }

这里再贴一下回文数字的解法9. 回文数 - 力扣（LeetCode）

public boolean isPalindrome(int x) {
        if(x<0){
            return false;
        }
        int temp = x;
        int cur = 0;
        while(temp > 0){
            cur = cur * 10 + temp % 10;
            temp/=10;
        }
        return x==cur;
    }

链表中使用递归

21. 合并两个有序链表 - 力扣（LeetCode）或者使用下面合并升序链表题型中的常规方法新建链表排序里的那种合并也行，这是同一道题。

使用递归实现，新链表也不需要构造新节点，我们下面列举递归三个要素

• 终止条件：两条链表分别名为 l1 和 l2，当 l1 为空或 l2 为空时结束
• 返回值：每一层调用都返回排序好的链表头
• 本级递归内容：如果 l1 的 val 值更小，则将 l1.next 与排序好的链表头相接，l2 同理
• O(m+n)O(m+n)，mm 为 l1的长度，nn 为 l2 的长度

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if(l1 == null) {
            return l2;
        }
        if(l2 == null) {
            return l1;
        }

        if(l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);//不断赋值连接
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }
}

二叉树转换为链表

114. 二叉树展开为链表 - 力扣（Leetcode）

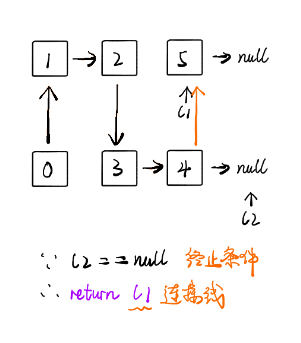
将一个二叉树转换为链表输出，并且为前序遍历，总的思路就是

    1
   / \
  2   5
 / \   \
3   4   6

//将 1 的左子树插入到右子树的地方
    1
     \
      2         5
     / \         \
    3   4         6        
//将原来的右子树接到左子树的最右边节点
    1
     \
      2          
     / \          
    3   4  
         \
          5
           \
            6
            
 //将 2 的左子树插入到右子树的地方
    1
     \
      2          
       \          
        3       4  
                 \
                  5
                   \
                    6   
        
 //将原来的右子树接到左子树的最右边节点
    1
     \
      2          
       \          
        3      
         \
          4  
           \
            5
             \
              6         

但是这里使用代码实现起来就是先将右子树拆接到左子树，然后再接到右子树上的

public void flatten(TreeNode root){
     while(root != null){ //切记要考虑当前节点的是否为null
        if(root.left == null){
            root = root.right;//已经为null了，直接考虑下一个
        }
        else{
            TreeNode tempTail = root.left;
            while(tempTail.right != null){//当执行到最后一个节点，注意这个判断
                tempTail = tempTail.right;//一直找左子树的最右边的节点
            }
            //这里先把右边接过去可以省去一个临时存储右子树的节点
            tempTail.right = root.right;
            root.right = root.left;
            root.left = null;
            root = root.right;//继续下一个节点
        }
     }
 }

相交的链表

160. 相交链表 - 力扣（LeetCode） 寻找两条链表相交的节点，一开始首先的想到的就是上面快慢的指针方法，但是实践一下哎，发现根本不可行，看到题解的这个方法恍然大悟，主要思路就是：使用双指针，是他们按相同的速度依次走一遍这两条链表(a先走a链表，b先走b链表)，路程相同，速度也相同，最后他们必然在终点的时候是相遇的，再往前推，最后一段路程是相同的，所以他们相遇的点即是交点，看到评论区的一句骚话：走到尽头见不到你，于是走过你来时的路，等到相遇时才发现，你也走过我来时的路。

 public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null){
            return null;
        } 
        ListNode pA = headA, pB = headB;
        while (pA != pB) {
            pA = pA == null ? headB : pA.next;
            pB = pB == null ? headA : pB.next;
        }
        return pA;
    }



// 若相交，链表A： a+c, 链表B : b+c. a+c+b+c = b+c+a+c 。则会在公共处c起点相遇。若不相交，a +b = b+a 。因此相遇处是NULL


// 下面这样写会导致若两条链表不相交，则会一直循环下去，导致超时
    //     while(cur != cur2){
    //         cur = cur.next;
    //         cur2 = cur2.next;
    //         if(cur == null){
    //             cur = headB;
    //         }
    //         if(cur2 == null){
    //             cur2 = headA;
    //         }
    //     }
    //     return cur;
    //    }

LRU 缓存

146. LRU 缓存 - 力扣（LeetCode） 做题的时候要形成条件反射，看到键值对就要想到HashMap，这里主要思路就是使用双向链表+哈希表，使用双向链表方便寻找头和尾，同时用哈希表的键和值来分别对应键和节点，每次生成键值对的时候，判断容量是否满了。每次将节点放在双向链表的最前面，如果访问了某一个节点，就把该节点移动到最前面，这样每次链表最后面的节点就是最近最久未使用的节点，当容量满了的时候，就删除替换这个节点即可。

面试官想看到的自己写双向链表和哈希表的版本

public class LRUCache {
    class DLinkedNode {
        int key;
        int value;
        DLinkedNode prev;
        DLinkedNode next;
        public DLinkedNode() {}
        public DLinkedNode(int _key, int _value) {key = _key; value = _value;}
    }
//使用双向链表+哈希表
    private Map<Integer, DLinkedNode> cache = new HashMap<Integer, DLinkedNode>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail;

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        // 使用伪头部和伪尾部节点
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }

    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            return -1;
        }
        // 如果 key 存在，先通过哈希表定位，再移到头部
        moveToHead(node);
        return node.value;
    }

    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            // 如果 key 不存在，创建一个新的节点
            DLinkedNode newNode = new DLinkedNode(key, value);
            // 添加进哈希表
            cache.put(key, newNode);
            // 添加至双向链表的头部
            addToHead(newNode);
            ++size;
            if (size > capacity) {
                // 如果超出容量，删除双向链表的尾部节点
                DLinkedNode tail = removeTail();
                //注意这里，看removeTail函数，这里的tail其实是倒数第二个，即我们插入的倒数第一个
                // 删除哈希表中对应的项
                cache.remove(tail.key);
                --size;
            }
        }
        else {
            // 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
            node.value = value;
            moveToHead(node);
        }
    }

    private void addToHead(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    private void moveToHead(DLinkedNode node) {
        removeNode(node);
        addToHead(node);
    }

    private DLinkedNode removeTail() {
        DLinkedNode res = tail.prev;
        removeNode(res);
        return res;
    }
}

Java帮你包好数据结构版本：

这里使用了Java封装好的LinkedHashMap结构，也就是我们上面写的那个结构，主要的思路就是继承该类，然后重写最近最少使用的节点的规则，把这个规则改成size大于容量的时候就删除就行，有关这个方法更加详细的解释可以参照源于 LinkedHashMap源码 - LRU 缓存 - 力扣（LeetCode）这个题解参考了部分源码，更容易理解

class LRUCache extends LinkedHashMap<Integer, Integer>{
    private int capacity;
    
    public LRUCache(int capacity) {
        super(capacity, 0.75F, true);
        //构造函数，0.75F指加载因子，使用默认就行，true代表按照读取的顺序，false(默认)则是按照插入顺序
        this.capacity = capacity;
    }

    public int get(int key) {
        return super.getOrDefault(key, -1);
    }

    // 这个可不写 因为题目要求相比父类的put方法并没有改变
    public void put(int key, int value) {
        super.put(key, value);
    }

    @Override
    protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
        return size() > capacity; //本题关键，删除最近最少使用的规则
    }
}

链表的排序

148. 排序链表 - 力扣（LeetCode） 看到题目所要求得log型时间复杂度，我们就应该想到使用归并排序

public ListNode sortList(ListNode head) {
        // 1、递归结束条件
        if (head == null || head.next == null) {
            //这里判断单节点的时候也是需要将head先写在前面，因为会先判断，避免空指针异常
            return head;
        }

        // 2、找到链表中间节点并断开链表 & 递归下探
        ListNode midNode = middleNode(head);
        ListNode rightHead = midNode.next;
        midNode.next = null;//斩断

        ListNode left = sortList(head);
        ListNode right = sortList(rightHead);

        // 3、当前层业务操作（合并有序链表）
        return mergeTwoLists(left, right);
    }
    
    //第一种方法 找到链表中间节点（876. 链表的中间结点）
    private ListNode middleNode(ListNode head) {
        if (head == null || head.next == null) {//单节点
            return head;
        }
        ListNode slow = head;
        ListNode fast = head.next.next;
        //没有做单双数区分，fast这里多走了一步
        //如果是单数节点会返回中间节点的前一个节点，因为主程序中该返回值返回后，还要+1，将真正的中间节点分到了后半段
        //但是因为是归并排序，所以没有影响
        //如果是偶数返回中间的前一个节点

        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }

        return slow;
    }

    //第二种写法这里区分了一下单双节点，单数节点返回中间，双数节点返回的前一个
    private ListNode midNode(ListNode head) {     
        ListNode fast = head;
        ListNode slow = head;
        while(fast != null){
            if(fast.next == null){
                return slow;//单数节点，返回真正的中间节点，相当于将中间节点分到了前一段
            }else if(fast.next != null && fast.next.next == null){//双数节点返回中间的前一个节点
                return slow;
            }else{
                fast = fast.next.next;
                slow = slow.next;
            }
        }
        return head;//上面循环没进去，说明是单个节点
    }

    // 合并两个有序链表（21. 合并两个有序链表）
    private ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode pre = new ListNode(-1);
        ListNode curr = pre;
        while(l1 != null && l2 != null) {
            if(l1.val < l2.val) {
                curr.next = l1;
                l1 = l1.next;
            } else {
                curr.next = l2;
                l2 = l2.next;
            }

            curr = curr.next;
        }

        curr.next = l1 != null ? l1 : l2;
        return pre.next;
    }

143. 重排链表 - 力扣（Leetcode）

题意：将链表重新排序为L(0) - L(n) - L(1) - L(n-1) - L(2) - L(n-2) - …的形式

思路：使用双指针分别从头尾遍历，然后重组链表,这种涉及到需要从单向链表的尾部往前遍历的，首先就应该考虑到使用集合来解决

美团一面的面试题

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public void reorderList(ListNode head) {
        List<ListNode> list = new ArrayList<>();
        ListNode cur = head;
        //存储到集合中
        while(cur != null){
            list.add(cur);
            cur = cur.next;
        }
        int i = 0;
        int j = list.size() - 1;
        while(i < j){
            list.get(i).next = list.get(j);
            i++;
            list.get(j).next = list.get(i);
            j--;
        }
        //记住末尾置空，防止环的出现
        list.get(i).next = null;
    }
}

//other version
class Solution {
    public void reorderList(ListNode head) {
        List<ListNode> list = new ArrayList<>();
        ListNode cur = head;
        while(cur != null){
            list.add(cur);
            cur = cur.next;
        }
        cur = head;
        int i = 1;
        int j = list.size() - 1;
        while(i <= j){
            ListNode nodeHead = list.get(i);
            ListNode nodeTail = list.get(j); 
            cur.next = nodeTail;
            cur.next.next = nodeHead;
            cur = cur.next.next;
            i++;
            j--;
        }
        cur.next = null;
    }
}

合并升序链表

先合并两个,就是和之前的归并里面的是一样的

剑指 Offer 25. 合并两个排序的链表 - 力扣（Leetcode）

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode pre = new ListNode(-1);
        ListNode cur = pre;
        while(l1 != null && l2 != null){
            if(l1.val < l2.val){
                cur.next = l1;
                l1 = l1.next;
                cur = cur.next;
            }else{
                cur.next = l2;
                l2 = l2.next;
                cur = cur.next;
            }
        }
        //注意这里顺序别搞错了
        cur.next = l1 == null ? l2 : l1;
        return pre.next;
    }
}

//have main
public class mergeTwoLists {
    public static ListNode buildList(ArrayList<Integer> list, int index) {
        // 如果已经处理完所有的元素，则返回null
        if (index >= list.size()) {
            return null;
        }
        // 创建一个新的节点，并且递归地为下一个节点调用此方法
        ListNode node = new ListNode(list.get(index), buildList(list, index + 1));
        return node;
    }
    public static ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(-1);
        ListNode cur = dummy;
        while (l1 != null && l2 != null) {
            if (l1.val <= l2.val) {
                cur.next = l1;
                l1 = l1.next;
            } else {
                cur.next = l2;
                l2 = l2.next;
            }
            cur= cur.next;
        }
        cur.next = l1 == null ? l2 : l1;
        return dummy.next;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();//链表节点个数
        ArrayList<Integer> list1 = new ArrayList<>();
        for(int i = 0;i < n;i++) {
            list1.add(scanner.nextInt());
        }
        ListNode l1 = buildList(list1,0);

        int m = scanner.nextInt();//链表节点个数
        ArrayList<Integer> list2 = new ArrayList<>();
        for(int i = 0;i < n;i++) {
            list2.add(scanner.nextInt());
        }
        ListNode l2 = buildList(list2,0);

        ListNode result = mergeTwoLists(l1,l2);
        while (result != null) {
            System.out.print(result.val + " ");
            result = result.next;
        }
    }
}

23. 合并K个升序链表 - 力扣（LeetCode）这道题刚看起来是个hard，但是一看题，感觉好像没有那么难，首先得思路就是和归并排序之前的一样合并，就是升级成K个而已，按照这个思路，写出了如下代码

public ListNode mergeKLists(ListNode[] lists) {
        ListNode temp = new ListNode();
        for(ListNode List:lists){
            temp.next =  merge(List,temp.next);//重复更新排序好的temp链表
        }
        return temp.next;
    }
    
    public ListNode merge(ListNode list1,ListNode list2){//常见的合并链表的方法  每次两个合并
        ListNode l1 = list1;
        ListNode l2 = list2;
        ListNode pre = new ListNode();
        ListNode cur = pre;
        while(l1 != null && l2 != null){
            if(l1.val<l2.val){
                cur.next = l1;
                cur = cur.next;
                l1 = l1.next;
            }else{
                cur.next = l2;
                cur = cur.next;
                l2 = l2.next;
            }
        }
        cur.next = l1 == null ? l2 : l1;
        return pre.next;
    }

//have main
public class mergeKLists {

    public ListNode mergeKLists(ListNode[] lists) {
        ListNode res = null;
        for(ListNode list : lists){
            res = merge(list,res);
        }
        return res;
    }

    public ListNode merge(ListNode l1,ListNode l2){
        ListNode pre = new ListNode(-1);
        ListNode cur = pre;
        while(l1 != null && l2 != null){
            if(l1.val < l2.val){
                cur.next = l1;
                l1 = l1.next;
            }else{
                cur.next = l2;
                l2 = l2.next;
            }
            cur = cur.next;
        }
        cur.next = l1 == null ? l2 : l1;
        return pre.next;
    }

    public static ListNode buildList(ArrayList<Integer> list, int index) {
        // 如果已经处理完所有的元素，则返回null
        if (index >= list.size()) {
            return null;
        }
        // 创建一个新的节点，并且递归地为下一个节点调用此方法
        ListNode node = new ListNode(list.get(index), buildList(list, index + 1));
        return node;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        //几条链表
        int n = sc.nextInt();
        ListNode[] lists = new ListNode[n];
        for (int i = 0; i < n; i++){
            int m = sc.nextInt();
            ArrayList<Integer> list = new ArrayList<>();
            for (int j = 0; j < m; j++){
                list.add(sc.nextInt());
            }
            ListNode head = buildList(list, 0);
            lists[i] = head;
        }
        mergeKLists mergeKLists = new mergeKLists();
        ListNode result = mergeKLists.mergeKLists(lists);
        while (result != null){
            System.out.print(result.val + " ");
            result = result.next;
        }
    }
}

虽然通过了，但是这种方法很明显，并不是很好

分治算法(归并排序) 这里的主要思路就是把lists[] 里面的一维的链表 看成是归并排序里面的一个数字，不断的分，最后两条链表合并的时候进行排序。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
   public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null || lists.length == 0){
           return null;  //首先需要考虑的当然是是否是空
        } 
        return merge(lists, 0, lists.length - 1);
    }

    public ListNode merge(ListNode[] lists, int left, int right) {
        if (left == right){//注意这里递归结束条件是不一样的
           return lists[left];   
        }
        int mid = (left + right) / 2;
        ListNode l1 = merge(lists, left, mid);//分
        ListNode l2 = merge(lists, mid + 1, right);//分
        return mergeTwoLists(l1, l2);//合
    }

    //这里合并采用的是上面的递归方法
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null){
            return l2;
        }  
        if (l2 == null){
            return l1;   
        }
        if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1,l2.next);
            return l2;
        }
    }
}

使用归并后，时间明显下降

栈

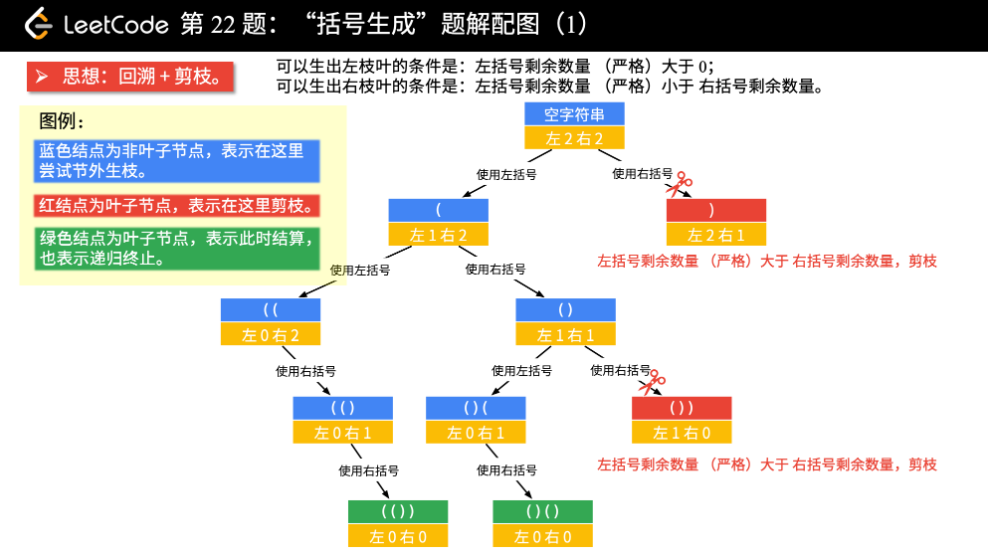
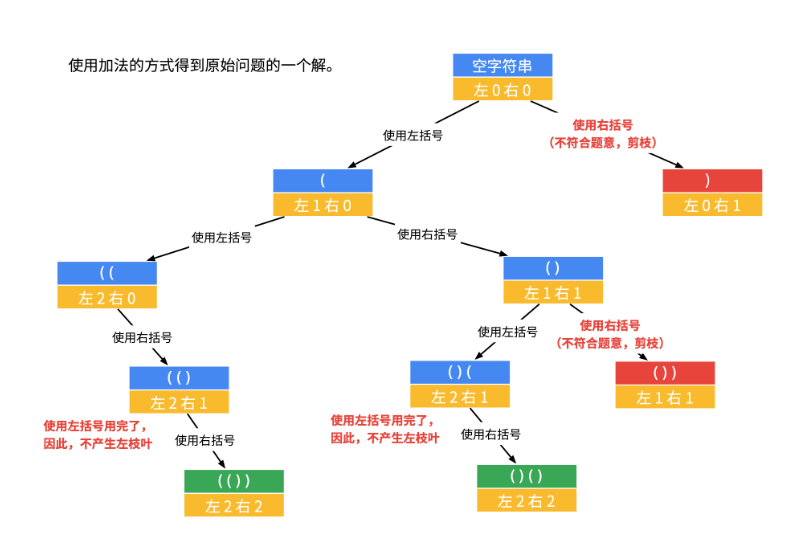
经典的括号匹配

20. 有效的括号 - 力扣（LeetCode）括号匹配的经典思路，遇到左括号直接入栈，如果遇到右括号，若栈为空，则不符合，若栈不为空，则出栈判断是否是匹配的那个括号，最后判断，栈里是否还有数据

public boolean isValid(String s) {
        if(s == null){
            return false;
        }
        char[] arr = s.toCharArray();//转变为数组
        Stack<Character> Stack = new Stack<Character>();
        for(char ch:arr){
            if(ch == '(' ||ch == '[' || ch == '{' ){
                Stack.push(ch);//遇到左括号直接入栈
            }else if(!Stack.isEmpty()){//栈不为空，遇到右括号，出栈对比
                char chpop = Stack.pop();
                if(chpop == '(' && ch!=')'){
                    return false;
                }
                if(chpop == '[' && ch!=']'){
                    return false;
                }
                if(chpop == '{' && ch!='}'){
                    return false;
                }
            }else if(Stack.isEmpty()){//栈为空 遇到右括号，不符合，直接返回
                return false;
            }

        }
        return Stack.isEmpty();//判断是否有落单的左括号
    }


//have main
public class isValid {
    public boolean isValid(String s) {
        if(s == null){
            return false;
        }
        char[] arr = s.toCharArray();//转变为数组
        Stack<Character> Stack = new Stack<Character>();
        for(char ch:arr){
            if(ch == '(' ||ch == '[' || ch == '{' ){
                Stack.push(ch);//遇到左括号直接入栈
            }else if(!Stack.isEmpty()){//栈不为空，遇到右括号，出栈对比
                char chpop = Stack.pop();
                if(chpop == '(' && ch!=')'){
                    return false;
                }
                if(chpop == '[' && ch!=']'){
                    return false;
                }
                if(chpop == '{' && ch!='}'){
                    return false;
                }
            }else if(Stack.isEmpty()){//栈为空 遇到右括号，不符合，直接返回
                return false;
            }

        }
        return Stack.isEmpty();//判断是否有落单的左括号
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        String s = scanner.nextLine();
        isValid isValid = new isValid();
        boolean valid = isValid.isValid(s);
        System.out.println(valid);
    }
}

下面贴一个鬼才代码，能通过，但是时间复杂度较高，本质是消消乐🤔

public boolean isValid(String s) {
        while(true){
            int l=s.length();//开始前量一次长度
            s=s.replace("()","");
            s=s.replace("{}","");
            s=s.replace("[]","");
            if(s.length()==l){//说明该消得已经消完了，本次循环没有再消
                return l==0;//判断是否落单
            }
        }
    }
    //代码鬼才

单调栈

739. 每日温度 - 力扣（LeetCode）简单的描述题，给你一个数组，找出当前位置后第一个比当前数字大的数字的与当前数字的距离，填在当前的位置上，先来看看暴力解法

//首先想到的是动规，但是我点的标签是栈emmm
    //发现动规好像并不可行，暴力好像可以
    public int[] dailyTemperatures(int[] temperatures) {
        int[] array = new int[temperatures.length];
        for(int i = 0;i<temperatures.length;i++){
            for(int j = i;j<temperatures.length;j++){
                if(temperatures[j] > temperatures[i]){//遇见第一个大于的温度
                   array[i] = j-i;
                   break;
                }
            }
        }
        return array;
    }

暴力解题，虽然可行，显著的问题就是效率不够高

单调栈的解法即维护一个存储下标的单调栈，从栈底到栈顶的下标对应的温度列表中的温度依次递减。如果一个下标在单调栈里，则表示尚未找到下一次温度更高的下标。每次入栈的时候与栈顶元素进行比较，如果当前的数值比栈顶元素小，直接入栈，反之若当前的数值比栈顶元素比大，说明找到了比它的值，则下标相减，得到间隔，然后将栈顶元素出栈，当前的元素继续与栈顶元素比较，重复上述步骤

视频讲解：LeetCode 图解 | 739.每日温度 - 每日温度 - 力扣（LeetCode）

note: 判别是否需要使用单调栈，如果需要找到左边或者右边第一个比当前位置的数大或者小，则可以考虑使用单调栈；单调栈的题目如矩形米面积等等

public int[] dailyTemperatures(int[] T) {
        Stack<Integer> stack = new Stack<Integer>();
        int[] result = new int[T.length];
        for(int i = 0;i<T.length;i++){//只需要循环一次，时间复杂度一下子就降下来了
            while(!stack.isEmpty() && T[stack.peek()]<T[i]){//栈里面只需要存储下标就行
                int pre = stack.pop();
                result[pre] = i - pre;
            }
            stack.add(i);
        }
        return result;
    }

时间复杂度：O(n)O(n)，其中 nn 是温度列表的长度。正向遍历温度列表一遍，对于温度列表中的每个下标，最多有一次进栈和出栈的操作。

空间复杂度：O(n)O(n)，其中 nn 是温度列表的长度。需要维护一个单调栈存储温度列表中的下标。

84. 柱状图中最大的矩形 - 力扣（LeetCode）给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积

柱状图中最大的矩形 题解思路：首先暴力会直接超时，因此类似的这种题可以考虑使用单调栈来进行解决

1. 单调栈：维护一个单调递增的栈，栈中保存柱子的索引。当遇到一个比栈顶元素高度小的柱子时，说明栈顶元素的右边界已经找到，此时弹出栈顶元素并计算其对应的矩形面积（如果不是比栈顶小的元素，说明还可以继续往右边截取，因此还没有到矩形的最大值）。
2. 左右边界确定：对于每个弹出的栈顶元素，其左边界是新的栈顶元素（若栈为空则为-1），右边界是当前遍历到的索引。遍历结束后，处理栈中剩余元素，其右边界设为数组长度n。
3. 面积计算：根据左右边界计算每个柱子对应的矩形面积，并更新最大值。

import java.util.Stack;

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        Stack<Integer> stack = new Stack<>();
        int maxArea = 0;
        
        for (int i = 0; i < n; i++) {
            //遇到比栈顶元素小的值，弹出并计算矩形的面积
            //这里使用循环就是为了像index=2;3在碰到下一个小的index=4,h=2的元素时都能出栈
            while (!stack.isEmpty() && heights[i] < heights[stack.peek()]) {
                int h = heights[stack.pop()];
                int left = stack.isEmpty() ? -1 : stack.peek();
                //真正的长度需要再减1，比如上图的index=3的6的面积就是4-2-1=1
                int width = i - left - 1;
                maxArea = Math.max(maxArea, h * width);
            }
            stack.push(i);
        }
        //开始处理还留在栈内的元素
        //遍历结束时，剩余元素的右侧没有更小的柱子，因此它们的右边界应视为数组末尾后的位置（即 n）
        while (!stack.isEmpty()) {
            int h = heights[stack.pop()];
            int left = stack.isEmpty() ? -1 : stack.peek();
            //所以这里的宽度都是为n来减
            int width = n - left - 1;
            maxArea = Math.max(maxArea, h * width);
        }
        
        return maxArea;
    }
}

接雨水也能用单调 栈的 解法，这个就后面再说了

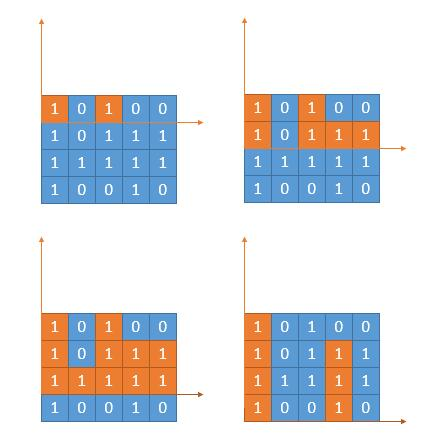
85. 最大矩形 - 力扣（LeetCode） 题意:给你下图所示的一个矩形，求出内部全部都为1的矩形的面积最大值

思路：这个题换一个思路就能变成和上一道题一样的题，具体的思路请看下图

通过不断的移动坐标系，使用84题中求出柱状图最大矩形的算法，就可以求出这一行中最大面积的矩形，把所有行都遍历完成，面积最大的那个矩形就是当前这个图内部全为1的最大矩形。因此只需要遍历每一行，存储1的高度数组，传给84题的函数，最后取最大值就可以了

class Solution {
    public int maximalRectangle(char[][] matrix) {
        int h = matrix.length;
        int w = matrix[0].length;
        int[] heights = new int[w];
        int maxArea = 0;
        for(int i = 0;i < h;i++){
            for(int j = 0;j < w; j++){
                if(matrix[i][j] == '1'){
                    heights[j]++;
                }else{
                    heights[j] = 0;
                }
            }
            maxArea = Math.max(maxArea,largestRectangleArea(heights));
        }
        return maxArea;
    }

    public int largestRectangleArea(int[] heights){
        int n = heights.length;
        int maxRowArea = 0;
        Stack<Integer> stack = new Stack<>();
        for(int i = 0;i < n;i++){
            while(!stack.isEmpty() && heights[i] < heights[stack.peek()]){
                //取出下标
                int h = heights[stack.pop()];
                int left = stack.isEmpty() ? -1 : stack.peek(); 
                int w = i - left - 1;
                maxRowArea = Math.max(maxRowArea, h * w) ;
            }
            //存储下标用于计算面积
            stack.push(i);
        }
        //处理剩下的元素
        while(!stack.isEmpty()){
            //取出下标
                int h = heights[stack.pop()];
                int left = stack.isEmpty() ? -1 : stack.peek(); 
                int w = n - left - 1;
                maxRowArea = Math.max(maxRowArea, h * w) ;
        }
        return maxRowArea;
    }
}

辅助栈

故名思意就是使用一个辅助的栈来解题，155. 最小栈 - 力扣（LeetCode），该题要求查找最小值的时候需要在常数的时间内完成，因此该题的思路就是，一个栈用来存储放入的数字，一个辅助的栈用来存储当前的最小值，每次进去的时候就会比较一次是否比栈顶的小，pop的时候就一起pop出去，这样栈顶的元素就是当前的栈元素里面的最小值。

class MinStack {

    Stack<Integer> stack1;
    Stack<Integer> stack2;


    public MinStack() {//构造函数初始化
       stack1 = new Stack<Integer>();
       stack2 = new Stack<Integer>();
       stack2.push(Integer.MAX_VALUE);
        //需要在一开始在辅助栈里面设置一个最大值
        //否则下面在比较的栈的最小值的时候会报错
    }
    
    public void push(int val) {
        stack1.push(val);
        stack2.push(Math.min(stack2.peek(),val));
    }
    
    public void pop() {
        stack1.pop();
        stack2.pop();
    }
    
    public int top() {
        return stack1.peek();
    }
    
    public int getMin() {
        return stack2.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(val);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

看到评论说面试官要求写一个不用辅助栈的，在这里贴一个

//本质上还是辅助栈，但是把辅助栈和元素栈合并在了一起


//方法一  栈里插数组
class MinStack {

    // 数组栈, [当前值, 当前最小值]
    private Stack<int[]> stack = new Stack<>();
    //还是第一次见到这样的
    public MinStack() {

    }

    public void push(int x) {
        if (stack.isEmpty()){
            stack.push(new int[]{x, x});//放入存储两位数字的数组，即数字和当前最小值
        }else {
            stack.push(new int[]{x, Math.min(x, stack.peek()[1])});
        }
    }

    public void pop() {
        stack.pop();
    }

    public int top() {
        return stack.peek()[0];
    }

    public int getMin() {
        return stack.peek()[1];
    }
}


//方法2  自定义链表
class MinStack {

    private Node node;

    public MinStack() {

    }

    public void push(int x) {
        if (node == null){
            node = new Node(x, x);
        }else {
            // node = new Node(x, Math.min(x, node.min), node);
            Node next = new Node(x, Math.min(x, node.min));
            next.prev = node;
            node = next;
        }
    }

    public void pop() {
        node = node.prev;
    }

    public int top() {
        return node.val;
    }

    public int getMin() {
        return node.min;
    }

    private class Node {
        int val;
        int min;
        Node prev;

        private Node(int val, int min){
            this.val = val;
            this.min = min;
        }

        private Node(int val, int min, Node prev){
            this.val = val;
            this.min = min;
            this.prev = prev;
        }
    }
}

//方法3  栈里面插入节点似乎也可行，这里就不细写了

辅助栈的另外一个应用394. 字符串解码 - 力扣（Leetcode）

构建辅助栈 stack， 遍历字符串 s 中每个字符 c；

• 当 c 为数字时，将数字字符转化为数字 multi，用于后续倍数计算；

• 当 c 为字母时，在 res 尾部添加 c；

• 当 c 为 [ 时，将当前 multi 和 res 入栈，并分别置空置 0：

  • 记录此 [ 前的临时结果 res 至栈，用于发现对应 ] 后的拼接操作；

  • 记录此 [ 前的倍数 multi 至栈，用于发现对应 ] 后，获取 multi × […] 字符串。

• 进入到新 [ 后，res 和 multi 重新记录。当 c 为 ] 时，stack 出栈，拼接字符串 res = last_res + cur_multi * res，其中:

  • last_res是上个 [ 到当前 [ 的字符串，例如 “3[a2[c]]” 中的 a；
  • cur_multi是当前 [ 到 ] 内字符串的重复倍数，例如 “3[a2[c]]” 中的 2。
    返回字符串 res

public String decodeString(String s) {
   StringBuilder res = new StringBuilder();
   int multi = 0;//用于后面乘数字
   LinkedList<Integer> stack_int =  new LinkedList<>();
   LinkedList<String> stack_str =  new LinkedList<>();
   for(Character c : s.toCharArray()){
       if(c == '['){//说明前面的数字和字母结束,可以入栈了
           stack_int.addLast(multi);//数字入栈
           stack_str.addLast(res.toString());//字符串入栈
           //记得置空
           res = new StringBuilder();
           multi = 0;
       }else if(c == ']'){
           StringBuilder tmp = new StringBuilder();
           int cur_int = stack_int.removeLast();//括号外的数字
           for(int i = 0; i < cur_int; i++) {//乘上几倍
               tmp.append(res);
           }
           res = new StringBuilder(stack_str.removeLast() + tmp);//和括号外的字母合并
       }else if(c >= '0' && c<= '9'){
           multi = multi * 10 + Integer.parseInt(c + "");//字符转换为数字
       }else{//为字母就追加
           res.append(c);
       }
   }
   return res.toString();
}

剑指 Offer 09. 用两个栈实现队列 - 力扣（Leetcode）

核心的思想就是使用A栈来增加元素，如果需要出队列了，就把元素倒过来又全部添加到B栈中，这样需要先出的元素就又到了栈顶，可以出队了

class CQueue {
    LinkedList<Integer> A,B;
    public CQueue() {
        A = new LinkedList<>();
        B = new LinkedList<>();
    }
    
    public void appendTail(int value) {
        A.addLast(value);
    }
    
    public int deleteHead() {
        //需要注意这里的判断的先后顺序
        if(!B.isEmpty()) return B.removeLast();
        //如果前面没有return，执行到后面就已经包含了一个隐含的条件B为空
        if(A.isEmpty()) return -1;
        while(!A.isEmpty()){
            B.addLast(A.removeLast());
        }
        return B.removeLast();
    }
}

/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue obj = new CQueue();
 * obj.appendTail(value);
 * int param_2 = obj.deleteHead();
 */

Stack版本

class CQueue {
    Stack<Integer> A,B;
    public CQueue() {
        A = new Stack<>();
        B = new Stack<>();
    }
    
    public void appendTail(int value) {
        A.push(value);
    }
    
    public int deleteHead() {
        if(!B.isEmpty()) return B.pop();
        //如果前面没有return，执行到后面就已经包含了一个隐含的条件B为空
        if(A.isEmpty()) return -1;
        while(!A.isEmpty()){
            B.push(A.pop());
        }
        return B.pop();
    }
}

/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue obj = new CQueue();
 * obj.appendTail(value);
 * int param_2 = obj.deleteHead();
 */

最长有效括号

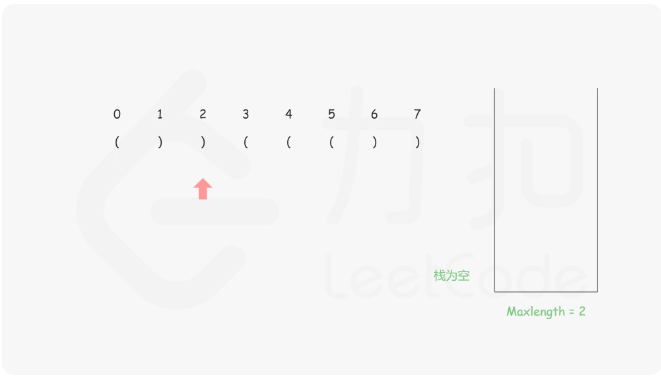
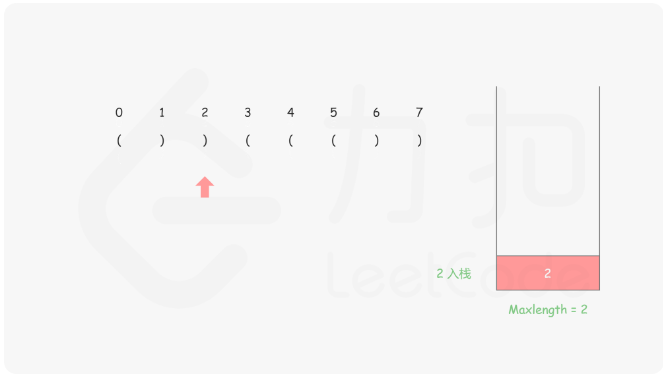
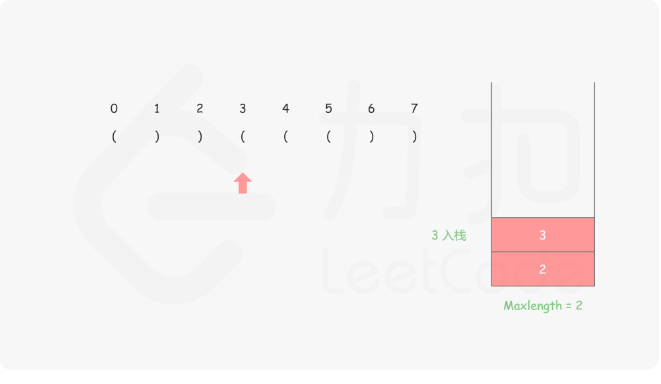
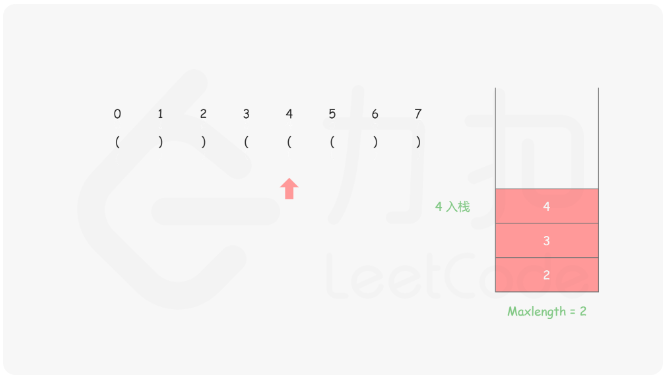
32. 最长有效括号 - 力扣（Leetcode）题目的要求大概就是寻找子串里符合（）且连续的最长的括号，思路好难，艹，完全想不到

栈做法

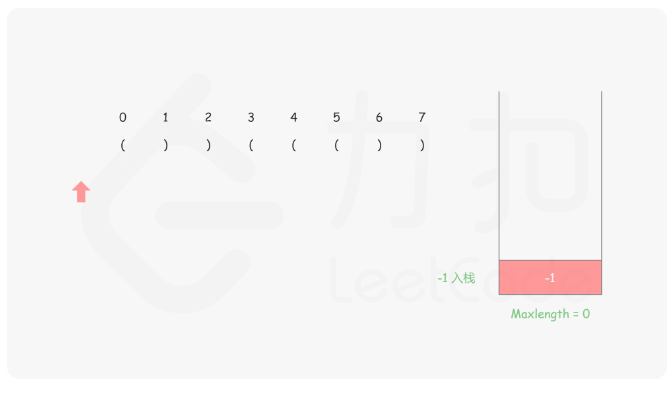
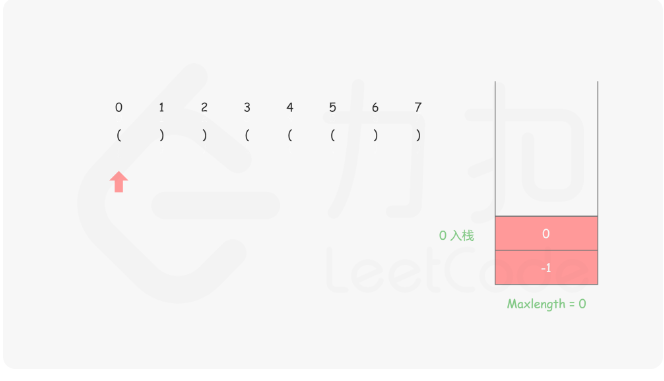
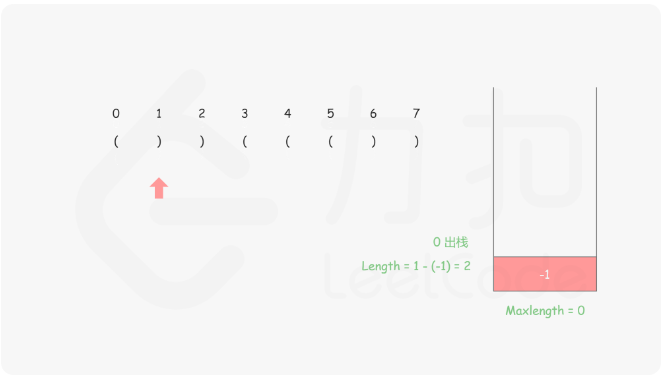
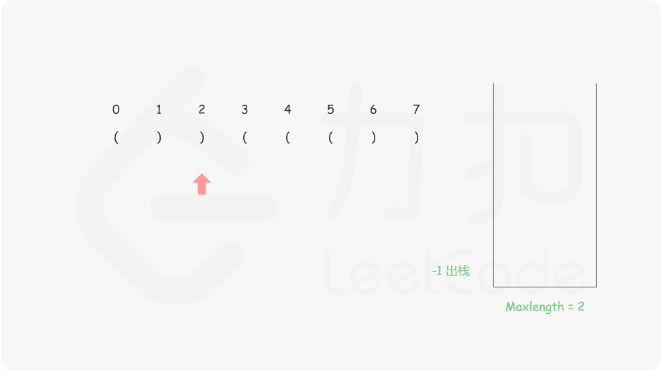
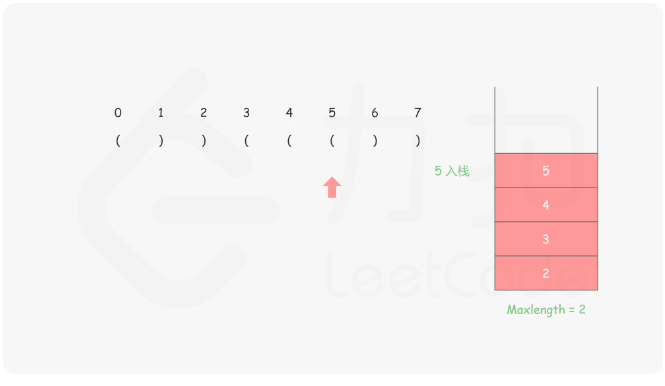
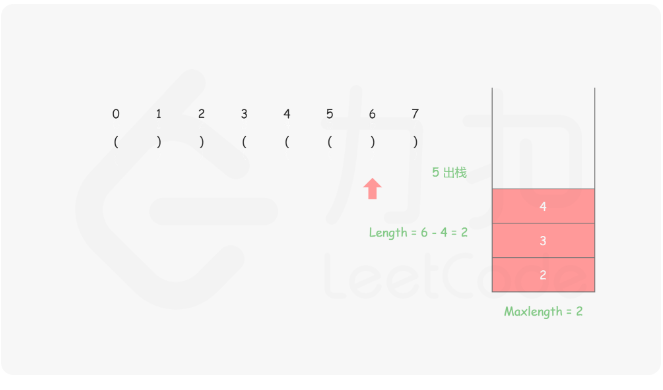
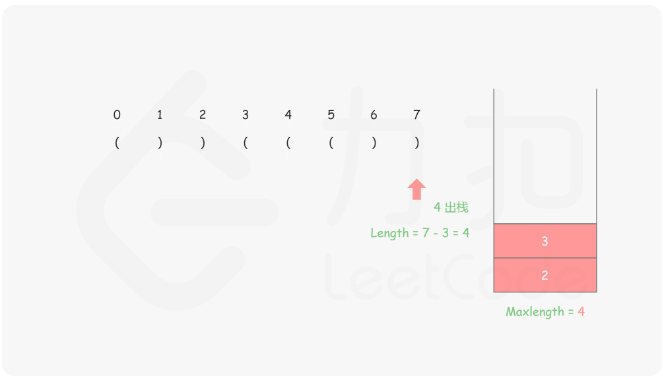
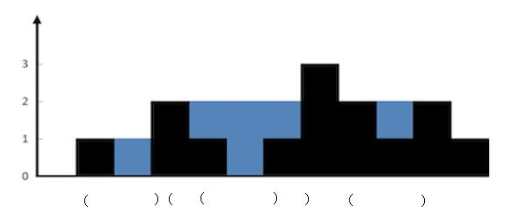
思路：首先我们需要保证栈底的元素是已经遍历的元素中最后一个未匹配的右括号，然后将左括号都入栈，每遇到右括号就出栈，然后减去当前栈顶的元素的下标就是这个右括号里面匹配了几个，具体的做法就是

• 对于遇到的每个‘(’，我们将它的下标放入栈中
• 对于遇到的每个')' ，我们先弹出栈顶元素表示匹配了当前右括号：
  • 如果栈为空，说明当前的右括号为没有被匹配的右括号，我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
  • 如果栈不为空，当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」

来看图示更好理解

//看到括号匹配啥的，首先想到的就是用栈
public int longestValidParentheses(String s) {
    Stack<Integer> stack = new Stack<>();
    int sum = 0;
    stack.push(-1);
    for(int i = 0;i < s.length();i++){//字符串的长度函数是有括号的
        if(s.charAt(i) == '('){
            stack.push(i);
        }else{
            stack.pop();
            if(stack.isEmpty()){
                stack.push(i);
            }else{
                sum = Math.max(sum,i - stack.peek());
            }
        }
    }
    return sum;
}

动态规划做法

思路和算法（说实话，没太看懂，待我再细细琢磨）

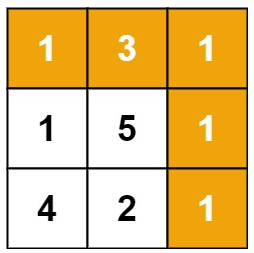
我们定义 dp[i] 表示以下标 i 字符结尾的最长有效括号的长度。我们将 dp 数组全部初始化为 0 。显然有效的子串一定以 ‘)’结尾，因此我们可以知道以 ‘(’ 结尾的子串对应的 dp 值必定为 0，我们只需要求解 ‘)’ 在 dp 数组中对应位置的值。

我们从前往后遍历字符串求解 dp 值，我们每两个字符检查一次：

1. s[i]=‘)’ 且 s[i−1]=‘(’，也就是字符串形如 “……()”，我们可以推出：

   dp[i]=dp[i−2]+2

2. s[i]=‘)’ 且s[i−1]=‘)’，也就是字符串形如 “……))”，我们可以推出： 如果 s[i−dp[i−1]−1]=‘(’，那么

   dp[i]=dp[i−1]+dp[i−dp[i−1]−2]+2

   我们考虑如果倒数第二个‘)’ 是一个有效子字符串的一部分（记作sub），对于最后一个‘)’ ，如果它是一个更长子字符串的一部分，那么它一定有一个对应的 ‘(’ ，且它的位置在倒数第二个‘)’ 所在的有效子字符串的前面（也就是 sub的前面）。因此，如果子字符串 sub的前面恰好是‘(’ ，那么我们就用 2 加上 sub的长度dp[i−1]去更新 dp[i]。同时，我们也会把有效子串 sub之前的有效子串的长度也加上，也就是再加上 dp[i−dp[i−1]−2]。最后的答案即为 dp 数组中的最大值。

public int longestValidParentheses(String s) {
       int maxans = 0;
       int[] dp = new int[s.length()];
       for (int i = 1; i < s.length(); i++) {
           if (s.charAt(i) == ')') {
               if (s.charAt(i - 1) == '(') {
                   dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
               } else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
                   dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
               }
               maxans = Math.max(maxans, dp[i]);
           }
       }
       return maxans;
   }

树

遍历

94. 二叉树的中序遍历 - 力扣（LeetCode）一道简单的中序遍历的题，唯一需要值得注意的就是返回的list

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<Integer>();
        infixOrder(root,list);
        return list;
    }

    public void infixOrder(TreeNode root,List<Integer> list){
        if(root == null){
            return;
        }
        infixOrder(root.left,list);
        list.add(root.val);//list集合用的是add，别记错了
        infixOrder(root.right,list);
    }
}

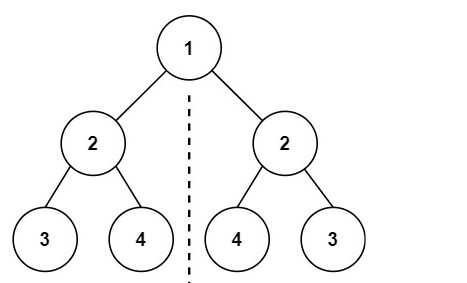
101. 对称二叉树 - 力扣（Leetcode）

题意：判断树是不是轴对称的

思路：使用递归遍历是不是对称的

class Solution {
	public boolean isSymmetric(TreeNode root) {
		if(root==null) {
			return true;
		}
		//调用递归函数，比较左节点，右节点
		return dfs(root.left,root.right);
	}
	
	boolean dfs(TreeNode left, TreeNode right) {
		//递归的终止条件是两个节点都为空
		//或者两个节点中有一个为空
		//或者两个节点的值不相等
		if(left==null && right==null) {
			return true;
		}
		if(left==null || right==null) {
			return false;
		}
		if(left.val!=right.val) {
			return false;
		}
		//再递归的比较 左节点的左孩子 和 右节点的右孩子
		//以及比较  左节点的右孩子 和 右节点的左孩子
		return dfs(left.left,right.right) && dfs(left.right,right.left);
	}
}

98. 验证二叉搜索树 - 力扣（Leetcode）

题意：就是验证这棵树是不是左子树的数据都小于当前节点，右子树的数据都大于当前的节点

思路：这里面有一个很重要的点，就是二叉搜索树的数据如果用中序遍历的话，遍历出来的数据是递增的，就比如下面的这棵树，因此我们可以使用中序遍历存储上一个节点的值，看是否是大于上一个节点，否则就不是二叉搜索树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    Integer pre;
    public boolean isValidBST(TreeNode root) {
       //访问到中点了，说明该子树是满足条件的
       if(root == null){
           return true;
       }
       //访问左子树
       boolean left = isValidBST(root.left);
       
       //访问当前节点，若为空说明还没有初始化，还需要初始化
       if(pre != null && root.val <= pre){
           return false;
       }
       //存储上一个节点的值
       pre = root.val;
       //访问右子树
       boolean right = isValidBST(root.right);

       return  left && right;
    }
}


//other version
class Solution {
    // 二叉搜索树的中序遍历都是递增的
    public boolean isValidBST(TreeNode root) {
        // integer的默认未初始化是null, int是0
        Integer[] preVal = new Integer[1];
        return infixOrder(root, preVal);
    }

    public boolean infixOrder(TreeNode node, Integer[] preVal) {
        if(node == null){
            return true;
        }
        // 遍历左子树
        boolean left = infixOrder(node.left, preVal);
        if (preVal[0] != null && preVal[0] >= node.val) {
            return false;
        }
        // 更新前一个节点的值为当前节点的值
        preVal[0] = node.val;
        // 遍历右子树
        boolean right = infixOrder(node.right, preVal);

        return left && right;
    }
}

543. 二叉树的直径 - 力扣（Leetcode）

简单的来说就是求二叉树深度的变形

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int ans = 0;
    public int diameterOfBinaryTree(TreeNode root) {
        depth(root);
        //根据题意，直径需要减一
        return ans - 1;
    }
    public int depth(TreeNode node) {
        if (node == null) {
            return 0; // 访问到空节点了，返回0
        }
        int L = depth(node.left); // 左儿子为根的子树的深度
        int R = depth(node.right); // 右儿子为根的子树的深度
        ans = Math.max(ans, L+R+1); // 计算d_node即L+R+1 并更新ans
        return Math.max(L, R) + 1; // 返回该节点为根的子树的深度
    }
}

617. 合并二叉树 - 力扣（Leetcode）

题意：将两个二叉树的节点合并起来，就是对应的节点的数据相加

思路：还是采用的通过同时遍历两棵树，如果有一方为空就返回

class Solution {
	public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
		if(t1==null || t2==null) {
			return t1==null? t2 : t1;
		}
		return dfs(t1,t2);
	}
	
	TreeNode dfs(TreeNode r1, TreeNode r2) {
		// 如果 r1和r2中，只要有一个是null，函数就直接返回
		if(r1==null || r2==null) {
			return r1==null? r2 : r1;
		}
		//让r1的值 等于  r1和r2的值累加，再递归的计算两颗树的左节点、右节点
		r1.val += r2.val;
		r1.left = dfs(r1.left,r2.left);
		r1.right = dfs(r1.right,r2.right);
		return r1;
	}
}

剑指 Offer 26. 树的子结构 - 力扣（LeetCode）

题意：一开始给你两棵树，A和B，请你判断B是不是A的一颗子树

思路：分别遍历A的每一个节点(使用一个函数)，并且同时以当前遍历的这个节点为根结点判断是不是和B这棵树一样，
一样就返回true，否则返回false

实现的细节：

• recur函数：使用recur函数对以节点A为根结点的树是否包含B进行判断，节点内的值不一致，显而易见的是false，若B为空，而A还有，说明已经判断完毕，返回true，若A为空而B还没有为空，则说明B还比A长，返回false
• 遍历每一个A节点的函数，先判断以根结点为A的树是否包含，如果没有包含，则继续递归的调用左子树和右子树，类似于树的前序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
 

class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B){
        //递归 不断
        if(A != null && B != null){
            if(recur(A,B)){
                return true;
            }else {
                return isSubStructure(A.left, B) || isSubStructure(A.right, B);
            }
        }else{
            return false;
        }
    }
    boolean recur(TreeNode A, TreeNode B) {
        if(B == null) return true;
        if(A == null || A.val != B.val) return false;
        return recur(A.left, B.left) && recur(A.right, B.right);
    }
}

124. 二叉树中的最大路径和 - 力扣（LeetCode）

题意：在二叉树中寻找任意一条路径，使得这条路径上的节点的值之和最大，路径可以是任意节点序列，只要相邻节点之间有边，且每个节点在路径中最多出现一次。

思路：

使用递归的方法来解决这个问题。对于每个节点，我们考虑两种情况：

1. 该节点作为路径的一部分，向上延伸。此时，只能选择左子树或右子树中的一个分支。
2. 该节点作为路径的最高点，此时可以同时包含左子树和右子树的路径。

具体步骤如下：

1. 递归遍历每个节点，计算以当前节点为根的单边最大路径和（即只能选择左或右子树的一个分支）。
2. 在递归过程中，计算当前节点作为中间节点的路径和（即左子树路径 + 当前节点值 + 右子树路径），并更新全局最大值。
3. 递归函数返回当前节点值加上左子树或右子树的最大路径和，以便继续向上延伸路径。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int maxSum = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        helper(root);
        return maxSum;
    }

    private int helper(TreeNode node) {
        if (node == null) {
            return 0;
        }
        // 递归计算左右子节点的最大贡献值，
        // 因为单个节点也可以作为一条路径，因此若为负则不计入，相当于舍弃负的这边
        int left = Math.max(helper(node.left), 0);
        int right = Math.max(helper(node.right), 0);
        
        // 当前节点作为路径中间节点的总路径和
        int currentPathSum = node.val + left + right;
        maxSum = Math.max(maxSum, currentPathSum);
        
        // 返回当前节点作为左子树或者右子树的最大贡献值（单边路径）
        return node.val + Math.max(left, right);
    }
}

建立树

105. 从前序与中序遍历序列构造二叉树 - 力扣（Leetcode）

题意：很明显，是根据前序和中序的遍历建立一个树

思路：我们知道，根据前序和中序遍历可以确定唯一一棵树

下面是使用的递归的方法创建这棵树，值得注意的是，题目说的是这棵树是没有重复的元素的

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 //感觉一道挺常规的题
 //递归
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return myBuildTreeHelper(preorder,0,preorder.length,inorder,0,inorder.length);
    }

    public TreeNode myBuildTreeHelper(int[] preorder,int p_start,int p_end,int[] inorder,int i_start,int i_end){
        if(p_start == p_end){
            return null;
        }

        int val = preorder[p_start];
        TreeNode root = new TreeNode(val);
        //头节点在中序遍历中的位置
        int i_index = -1;
        //注意题目说的是没有重复元素的哦
        for(int i = 0;i < inorder.length;i++){
            if(inorder[i] == val){
                i_index = i;
                break;
            }
        }
        //左子树有几个元素
        int leftnum = i_index - i_start;
        //开始递归
        //前序遍历中，左子树就是刚刚的start+1到加上刚刚的左子树元素+1，由于上面是index-start所以需要中序遍历的中间节点放在左边
        root.left  = myBuildTreeHelper(preorder,p_start+1,p_start+leftnum+1,inorder,i_start,i_index);
        root.right = myBuildTreeHelper(preorder,p_start+leftnum+1,p_end,inorder,i_index+1,i_end);
        return root;
    }
}

由于还需要每次遍历去找中序遍历的中间节点，所以这里可以采用hash来优化一下下

public TreeNode buildTree(int[] preorder, int[] inorder) {
    HashMap<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < inorder.length; i++) {
        map.put(inorder[i], i);
    }
    return buildTreeHelper(preorder, 0, preorder.length, inorder, 0, inorder.length, map);
}

private TreeNode buildTreeHelper(int[] preorder, int p_start, int p_end, int[] inorder, int i_start, int i_end,
                                 HashMap<Integer, Integer> map) {
    if (p_start == p_end) {
        return null;
    }
    int root_val = preorder[p_start];
    TreeNode root = new TreeNode(root_val);
    int i_root_index = map.get(root_val);
    int leftNum = i_root_index - i_start;
    root.left = buildTreeHelper(preorder, p_start + 1, p_start + leftNum + 1, inorder, i_start, i_root_index, map);
    root.right = buildTreeHelper(preorder, p_start + leftNum + 1, p_end, inorder, i_root_index + 1, i_end, map);
    return root;
}

剑指 Offer 07. 重建二叉树 - 力扣（Leetcode）

使用递归

最核心的思想就是使用前序来确定根节点，中序来确定左子树和右子树的根节点，所以说这里的根节点是在前序遍历里的，左子节点和右子节点是在中序遍历里面的

	根节点索引	中序遍历左边界	中序遍历右边界
左子树	root + 1	left	i - 1
右子树	i - left + root + 1	i + 1	right

这里的 i 就是在中序中上一个根节点的位置，而在表中右子树的(注意根节点的位置是在前序中遍历)i - left + root + 1指的就是左子树的长度(i-left) 加上根节点的位置在加上1

剑指 Offer 07. 重建二叉树 - 更加详细的题解

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int[] preorder;
    HashMap<Integer, Integer> dic = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        for(int i = 0; i < inorder.length; i++){
            dic.put(inorder[i],i);
        }
        return recur(0, 0, inorder.length - 1);
    }
    TreeNode recur(int root, int left, int right) {
        if(left > right){
            return null;
        }
        TreeNode node = new TreeNode(preorder[root]);
        int i = dic.get(preorder[root]);
        node.left  = recur(root + 1, left, i - 1);
        node.right = recur(i - left + root + 1, i + 1, right);
        return node;
    }
}

依靠推导公式解决

这种题，面试出题总不可能现场推导吧，时间太慢，记住就行

96. 不同的二叉搜索树 - 力扣（Leetcode）

题意：给你一个数字，问你形状不同的二叉搜索树形状有多少个

使用动态规划，这里需要推导一下递推公式

• 假设 n 个节点存在二叉排序树的个数是 G (n)，令 f(i) 为以 i 为根的二叉搜索树的个数，则

​ G(n)=f(1)+f(2)+f(3)+f(4)+…+f(n)

• 当 i 为根节点时，其左子树节点个数为 i-1 个，右子树节点为 n-i，则

​ **f(i)=G(i−1)∗G(n−i) **

• 综合两个公式可以得到 卡特兰数 公式
  G(n)=G(0)∗G(n−1)+G(1)∗(n−2)+…+G(n−1)∗G(0)

class Solution {
    //卡特兰数公式
    public int numTrees(int n) {
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;

        for(int i = 2;i < n + 1;i++){
            for(int j = 1;j < i + 1;j++){
                dp[i] += dp[j-1] * dp[i-j];
            }
        }
        return dp[n];
    }
}

或者来个取巧的方法

class Solution {
    public int numTrees(int n) {
         switch(n){
            case 1: return 1;
            case 2: return 2;
            case 3: return 5;
            case 4: return 14;
            case 5: return 42;
            case 6: return 132;
            case 7: return 429;
            case 8: return 1430;
            case 9: return 4862;
            case 10: return 16796;
            case 11: return 58786;
            case 12: return 208012;
            case 13: return 742900;
            case 14: return 2674440;
            case 15: return 9694845;
            case 16: return 35357670;
            case 17: return 129644790;
            case 18: return 477638700;
            case 19: return 1767263190;
            default: return 0;
        }
    }
}

前缀树

题意：实现一个前缀树，效果需要

请你实现 Trie 类：

• Trie() 初始化前缀树对象。
• void insert(String word) 向前缀树中插入字符串 word 。
• boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
• boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false

208. 实现 Trie (前缀树) 题解

相当于一个26叉树

插入字符串

我们从字典树的根开始，插入字符串。对于当前字符对应的子节点，有两种情况：

• 子节点存在。沿着指针移动到子节点，继续处理下一个字符。
• 子节点不存在。创建一个新的子节点，记录在 children 数组的对应位置上，然后沿着指针移动到子节点，继续搜索下一个字符。

重复以上步骤，直到处理字符串的最后一个字符，然后将当前节点标记为字符串的结尾。

查找前缀

我们从字典树的根开始，查找前缀。对于当前字符对应的子节点，有两种情况：

• 子节点存在。沿着指针移动到子节点，继续搜索下一个字符。
• 子节点不存在。说明字典树中不包含该前缀，返回空指针。
  重复以上步骤，直到返回空指针或搜索完前缀的最后一个字符

class Trie {
    private Trie[] children;
    private boolean isEnd;

    public Trie() {
        children = new Trie[26];
        isEnd = false;
    }
    
    public void insert(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            char ch = word.charAt(i);
            int index = ch - 'a';
            if (node.children[index] == null) {
                node.children[index] = new Trie();
            }
            node = node.children[index];
        }
        node.isEnd = true;
    }
    
    public boolean search(String word) {
        Trie node = searchPrefix(word);
        return node != null && node.isEnd;
    }
    
    public boolean startsWith(String prefix) {
        return searchPrefix(prefix) != null;
    }

    private Trie searchPrefix(String prefix) {
        Trie node = this;
        for (int i = 0; i < prefix.length(); i++) {
            char ch = prefix.charAt(i);
            int index = ch - 'a';
            if (node.children[index] == null) {
                return null;
            }
            node = node.children[index];
        }
        return node;
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

数组

自定义排序

//降序
Arrays.sort(arr, new Comparator<Integer>() {
    //重写compare方法，最好加注解，不加也没事
    public int compare(Integer a, Integer b) {
        //返回值>0交换
        return b-a;
    }
});

//降序
Arrays.sort(arr, (a, b) -> {return b-a;});

连续子数组

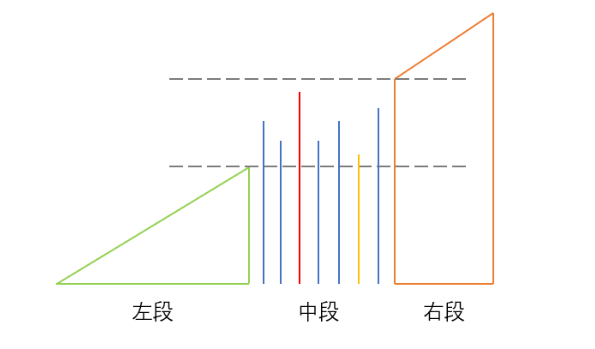
581. 最短无序连续子数组 - 力扣（Leetcode）这道题还是比较靠思维，下面贴一张图比较好懂

先只考虑中段数组，设其左边界为L，右边界为R：

• nums[R] 不可能是【L，R】中的最大值（否则应该将 nums[R] 并入右端数组）
• nums[L] 不可能是【L，R】中的最小值（否则应该将 nums[L] 并入左端数组）

很明显:

• 【L，R】中的最大值 等于【0，R】中的最大值，设其为 max
• 【L，R】中的最小值 等于 【L， nums.length-1】中的最小值，设其为 min

那么有：

• nums[R] < max < nums[R+1] < nums[R+2] < … 所以说，从左往右遍历，最后一个小于max的为右边界
• nums[L] > min > nums[L-1] > nums[L-2] > … 所以说，从右往左遍历，最后一个大于min的为左边界

//只能说是题解牛逼
    public int findUnsortedSubarray(int[] nums) {
        int len = nums.length;
        int begin = 0;//左边界
        int end = -1;//右边界
        int max = nums[0];
        int min = nums[len-1];

        for(int i = 0;i<len;i++){
            //从左到右维护最大值，最后一个小于最大值的就是右边界
            if(nums[i] < max){
                end = i;
            }else{
                max = nums[i];
            }

            //从右到左维护最小值，最后一个大于最小值的就是左边界
            if(nums[len-i-1] > min){
                begin = len-i-1;
            }else{
                min = nums[len-i-1];
            }
        }

        return end-begin+1;
    }

接雨水

42. 接雨水 - 力扣（Leetcode）一个hard题，字节好像很喜欢考这个题，我自己做的时候感觉也出现过好多次了，之前千峰杯还是啥比赛做过，可惜现在还是不会😥

解法一，按照行求(不建议使用)

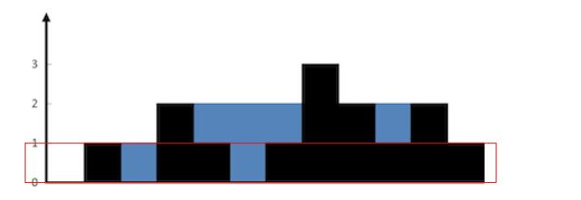
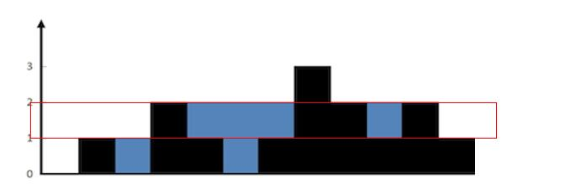
思路：一行一行的找，当遇到一个大于等于层数的墙时，开始记录，后面每当遇到一个小于层数的墙，雨水temp就加一，然后又遇到大于等于层数的墙的时候，将temp加到最终 答案ans上，否则不加，以此类推到每一层

// 按照行来求
public int trap(int[] height) {
    int ans = 0;
    int max = getMax(height);
    for(int i = 1;i < max;i++){ //从第一行开始
        int temp = 0;
        boolean isStart = false; //是否开始记录的标志
        for (int j = 0; j < height.length; j++) {
            if (isStart && height[j] < i) {
                temp++;
            }
            if (height[j] >= i) {
                ans = ans + temp;
                temp = 0;
                isStart = true;
            }
        }
    }
    return ans;
}

private int getMax(int[] height){
    int max = -1;
    for(int i = 0;i<height.length;i++){
        if(height[i] > max){
            max = height[i];
        }
    }
    return max;
}

为什么这个不建议使用呢，首先，这确实时最容易想到的方法，思路也没有错，但是会超出时间限制😥

解法二，按列来

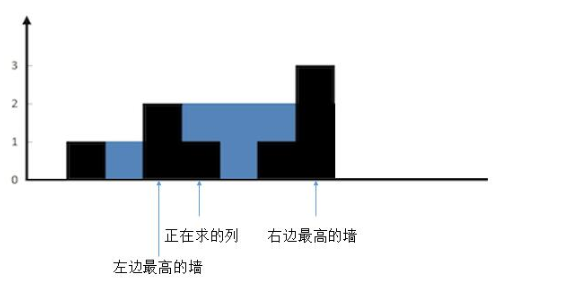
思路：我们单独的来看一列，，然后找出这一列左边最高的一列和右边最高的一列，而左右最高的墙中较矮的墙相对于当前的列，无非下面三种情况

• 较矮的墙大于当前的墙

去掉多余的列

可以看出这种情况的话，当前的列上面是有水的，可以计算出有(leftMax - 当前的列)单位的水

• 较矮的墙小于当前的高度

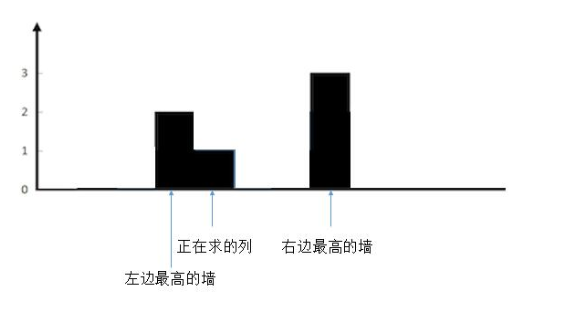
这种情况很明显，当前的墙上面是不会有积水的

• 较矮的墙等于当前的高度

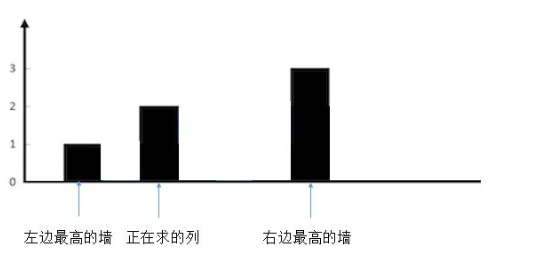
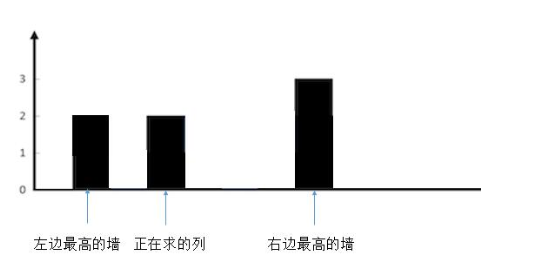
这种情况同理，也不会有积水

// 按照列来求
public int trap(int[] height) {
    int ans = 0;
    //左右两边是肯定没有水的
    for(int i = 0;i<height.length;i++){
        //找出左边最高
        int leftMax = -1;
        for(int j = 0;j < i; j++){
            if(height[j] > leftMax){
                leftMax = height[j];
            }
        }

        //找出右边最高
        int rightMax = -1;
        for(int k = i;k < height.length; k++){
            if(height[k] > rightMax){
                rightMax = height[k];
            }
        }

        int min = Math.min(leftMax,rightMax);
        //当前的节点比左右最高中较矮的那个矮才能有水
        if(min > height[i]){
            ans = ans + (min - height[i]);
        }
    }
    return ans;
}

解法三 动态规划

思路：主要思路和上面的一样，不同是使用动态规划来优化了寻找左右两边最高的墙的操作

• leftMax[i]表示左边最高的墙的高度，那么这个高度可以通过前面的值来计算，左边最高墙的值就等于前一个左边最高墙的值和左边一格墙的值中，较高的那个，那么有leftMax[j] = Math.max(leftMax[j - 1],height[j - 1]);
• 同理，右边墙的最高值有 rightMax[k] = Math.max(rightMax[k + 1],height[k + 1]);

// 按照列来求
//使用动归来优化
public int trap(int[] height) {
    int ans = 0;
    int[] leftMax = new int[height.length];
    int[] rightMax = new int[height.length];
    //找出左边最高
    for(int j = 1;j < height.length - 1; j++){
        leftMax[j] = Math.max(leftMax[j - 1],height[j - 1]);
    }

    //找出右边最高
    for(int k = height.length - 2;k > 0; k--){
        rightMax[k] = Math.max(rightMax[k + 1],height[k + 1]);
    }

    //左右两边是肯定没有水的
    for(int i = 0;i<height.length;i++){

        int min = Math.min(leftMax[i],rightMax[i]);
        //当前的节点比左右最高中较矮的那个矮才能有水
        if(min > height[i]){
            ans = ans + (min - height[i]);
        }
    }
    return ans;
}

解法四 栈

思路：有点类似于括号匹配，总体的原则就是

• 当前高度小于等于栈顶的高度，入栈，指针后移
• 当前高度大于栈顶高度，出栈，计算当前墙和栈顶的墙之间的多少，然后计算当前的高度和新栈的高度的关系，重复第 2 步。直到当前墙的高度不大于栈顶高度或者栈空，然后把当前墙入栈，指针后移。
• 而对于计算 current 指向墙和新的栈顶之间的水，根据图的关系，我们可以直接把这两个墙当做之前解法三的 max_left 和 max_right，然后之前弹出的栈顶当做每次遍历的 height [ i ]。水量就是 Min ( max _ left ，max _ right ) - height [ i ]，只不过这里需要乘上两个墙之间的距离

//使用栈
//使用栈的计算过程没有之前几个好理解
public int trap(int[] height) {
    int sum = 0;
    Stack<Integer> stack = new Stack<>();
    int current = 0;//从0开始遍历
    while(current < height.length){
        while( !stack.isEmpty() && height[stack.peek()] < height[current]){//判断empty要放前面，不然报栈空异常
            int h = height[stack.peek()];
            stack.pop();//出栈
            if(stack.isEmpty()){
                break;
            }
            int distance = current - stack.peek() - 1;
            
            //这里peek的元素已经是刚刚出栈元素的前一个元素了
            int min = Math.min(height[stack.peek()],height[current]);
            //需要乘上distance是因为不一定是挨着的
            sum += distance * (min - h); 
        }
        stack.push(current); //当前指向的墙入栈
        current++; //指针后移
    }
    return sum;
}

还有一种双指针的没看太懂，就先不写了，我是菜鸡

双指针

11. 盛最多水的容器 - 力扣（Leetcode）和接雨水好像有点像，但是又有点不像👀，一开始见到就有思路，就是暴力，虽然样例是可以过的，但是果不其然会超出时间限制，这里还是贴一下

//初见 暴力
public int maxArea(int[] height) {
    int max = -1;
    for(int i = 0;i<height.length;i++){
        for(int j = i+1;j<height.length;j++){
            max = Math.max(max,(j-i)*Math.min(height[i],height[j]));
        }
    }
    return max;
}

双指针解法

水的体积公式由题可知： S(i,j)=min(h[i],h[j])×(j−i)

在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽 底边宽度 −1 变短：

若向内 移动短板 ，水槽的短板 min(h[i],h[j]) 可能变大，因此下个水槽的面积 可能增大 。
若向内 移动长板 ，水槽的短板 min(h[i],h[j]) 不变或变小，因此下个水槽的面积 一定变小 。

因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。

//尝试动规 //失败
//更推荐双指针
public int maxArea(int[] height) {
    int waterMax = -1,i = 0,j = height.length - 1;
    while(i < j){
        waterMax = height[i] < height[j] ? 
            Math.max(waterMax,(j - i) * height[i++]) : //短板向内收缩
            Math.max(waterMax,(j - i) * height[j--]) ;
    }
    return waterMax;
}

//几行代码就搞定，简直是优雅

//have main
public class container_with_most_wate {
    public static int maxArea(int[] height) {
        //短板向内进行收缩
        int waterMax = -1,left = 0,right = height.length - 1;
        while(left!=right){
            waterMax = height[left] > height[right] ?
                    Math.max(waterMax,(right-left) * height[right--]):
                    Math.max(waterMax,(right-left) * height[left++]);
        }
        return waterMax;
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        //输入容器长度
        int len = scanner.nextInt();
        int[] height = new int[len];
        for(int i = 0;i < len;i++){
            //输入全部容器的高度
            height[i] = scanner.nextInt();
        }
        System.out.println(maxArea(height));
    }
}

15. 三数之和 - 力扣（Leetcode）双指针的又一个应用，题意是要你找出三个不同的数，并且相加等于0,同时不能重复

思路：排序后在当前数字的后面使用两个指针从两边(i+1，length-1)开始找,同时在找的时候还需要去重，其中有以下几种情况需要特判

• nums.length<3 都凑不齐三个数字，当然直接返回
• nums[i] > 0 因为是已经排序过了，所以后面的数字都大于0 ，不可能在相加等于0，直接返回

class Solution {
    //不可重复 set?
    //三个数互不相等 但是相加等于0
    //双指针？
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> lists = new ArrayList<>();//最终返回的结果
        //特判
        if(nums.length<3){
            return lists;
        }

        Arrays.sort(nums);
        for(int i = 0;i<nums.length;i++){
            //特判
            if(nums[i]>0) return lists;
            //去重
            if(i > 0 && nums[i] == nums[i-1]) continue;

            //双指针
            int left = i + 1,right = nums.length - 1;            
            while(left<right){
                int sum = nums[i] + nums[left] + nums[right];
                if( sum == 0){
                    List<Integer> list = new ArrayList<>();
                    list.add(nums[i]);//记住这里add的是数字不是下标，淦
                    list.add(nums[left]);
                    list.add(nums[right]);
                    lists.add(list);
                    //去重
                    while(left<right && nums[left] == nums[left+1])  left++;
                    while(left<right && nums[right] == nums[right-1])  right--;   
                    left++;
                    right--;
                }else if(sum<0){
                    //和小于零移动左指针，因为右边值更大
                    left++;
                }else{
                    //和大于零移动右指针，因为左边边值更小
                    right--;
                }
                
            }
        }
        return lists;
    }
}


//have main
public class threeSum {
    //不可重复 set?
    //三个数互不相等 但是相加等于0
    //双指针？
    public static List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> lists = new ArrayList<>();//最终返回的结果
        //特判
        if(nums.length<3){
            return lists;
        }

        Arrays.sort(nums);
        for(int i = 0;i<nums.length;i++){
            //特判
            if(nums[i]>0) return lists;
            //去重
            if(i > 0 && nums[i] == nums[i-1]) continue;

            //双指针
            int left = i + 1,right = nums.length - 1;
            while(left<right){
                int sum = nums[i] + nums[left] + nums[right];
                if( sum == 0){
                    List<Integer> list = new ArrayList<>();
                    list.add(nums[i]);//记住这里add的是数字不是下标，淦
                    list.add(nums[left]);
                    list.add(nums[right]);
                    lists.add(list);
                    //去重
                    while(left<right && nums[left] == nums[left+1])  left++;
                    while(left<right && nums[right] == nums[right-1])  right--;
                    left++;
                    right--;
                }else if(sum<0){
                    //和小于零移动左指针，因为右边值更大
                    left++;
                }else{
                    //和大于零移动右指针，因为左边边值更小
                    right--;
                }

            }
        }
        return lists;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int len = scanner.nextInt();
        int[] nums = new int[len];
        for (int i = 0; i < len; i++) {
            nums[i] = scanner.nextInt();
        }
        List<List<Integer>> result = threeSum(nums);
        //直接打印集合
        System.out.println("结果: " + result);
    }
}

75. 颜色分类 - 力扣（Leetcode）荷兰国旗问题

题意：把0，1，2三个数字按照大小排序，并使相同的元素相邻

思路：其实完全可以用排序解决

方法一：各种排序算法，这里不细说

方法二：单指针

使用一个指针，用来记录头部的位置，第一次循环，每次一遇到0，就交换到头部，同时指针加一。第二次循环从头部的位置开始，一遇到1就交换，把一交换到中间位置。

public void sortColors(int[] nums) {
    int prepointer = 0;//记录头部位置
    for(int i = 0;i < nums.length;i++){
        if(nums[i] == 0){
            int temp = nums[prepointer];
            nums[prepointer]  = nums[i];
            nums[i] = temp;
            prepointer++;//全部交换到了头部
        }
    }
    for(int i = prepointer;i < nums.length;i++){
        if(nums[i] == 1){
            int temp = nums[prepointer];
            nums[prepointer]  = nums[i];
            nums[i] = temp;
            prepointer++;//把一全部交换到了中间位置
        }
    }
}

//单指针交换0和2
class Solution {
    //单指针
    public void sortColors(int[] nums) {
        int p0 = 0,p2 = nums.length-1; 
        for(int i = 0;i < nums.length;i++){
            if(nums[i]==0){
                //和头部交换
                int temp = nums[i];
                nums[i] = nums[p0];
                nums[p0] = temp;
                p0++;
            }
        }
        for(int i = nums.length - 1;i >= 0;i--){
            if(nums[i]==2){
                //和尾部交换
                int temp = nums[i];
                nums[i] = nums[p2];
                nums[p2] = temp;
                p2--;
            }
        }
    }
}


//have main
public class sortColors {
    //也可以直接使用排序算法
    public static void sortColors(int[] nums) {
        int p0 = 0,p2 = nums.length-1;
        for(int i = 0;i < nums.length;i++){
            if(nums[i]==0){
                //和头部交换
                int temp = nums[i];
                nums[i] = nums[p0];
                nums[p0] = temp;
                p0++;
            }
        }
        for(int i = nums.length - 1;i >= 0;i--){
            if(nums[i]==2){
                //和尾部交换
                int temp = nums[i];
                nums[i] = nums[p2];
                nums[p2] = temp;
                p2--;
            }
        }
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] nums = new int[n];
        for(int i = 0;i<n;i++){
            nums[i] = sc.nextInt();
        }
        sortColors(nums);
        System.out.println(Arrays.toString(nums));
    }
}

方法三：双指针

双指针法，一个在前交换0，一个在后交换2

• 如果找到了0，那么与前面两种方法类似，将其与nums[p0] 进行交换，并将 p0向后移动一个位置；

• 如果找到了2，那么将其与 nums[p2]进行交换，并将 p2向前移动一个位置。

可以发现，对于第二种情况，当我们将 nums[i] 与 nums[p2] 进行交换之后，新的 nums[i] 可能仍然是 2，也可能是 0。然而此时我们已经结束了交换，开始遍历下一个元素nums[i+1]，不会再考虑 nums[i] 了，这样我们就会得到错误的答案。

因此，当我们找到 2 时，我们需要不断地将其与 nums[p2] 进行交换，直到新的 nums[i] 不为 2。此时，如果nums[i]为 0，那么对应着第一种情况；如果 nums[i] 为1，那么就不需要进行任何后续的操作。

class Solution {
    public void sortColors(int[] nums) {
        int n = nums.length;
        int p0 = 0, p2 = n - 1;
        for (int i = 0; i <= p2; ++i) {
            while (i <= p2 && nums[i] == 2) {
                int temp = nums[i];
                nums[i] = nums[p2];
                nums[p2] = temp;
                --p2;
            }
            if (nums[i] == 0) {
                int temp = nums[i];
                nums[i] = nums[p0];
                nums[p0] = temp;
                ++p0;
            }
        }
    }
}

283. 移动零 - 力扣（Leetcode）一道简单题,但是我们依然可以使用双指针来简化时间，优化算法283. 移动零题解

先看看普通的解法，就是通过两次遍历，(其实也还是双指针)把非0的元素都换到前面去，记录下位置，再把后面的元素都赋为0即可，需要两次遍历

class Solution {
    public void moveZeroes(int[] nums) {
        int j = 0;
        for(int i = 0;i<nums.length;i++){
            if(nums[i]!=0){
                nums[j++] = nums[i];
            }
        }
        while(j <= nums.length - 1){
            nums[j++] = 0;
        }
    }
}

我们可以通过双指针优化，使用一次遍历即可完成

第二种解法的本质是一个循环不变量：在每一次循环前，j 的左边全部都是不等于0的

• 起始j为0，明显满足
• 此后每一次循环中，若nums[i] = 0，则j保持不变，满足；若nums[i] != 0，交换后j增一，仍然满足

这就保证了最后结果的正确性。

class Solution {
    public void moveZeroes(int[] nums) {
        int j = 0;
        for(int i = 0;i<nums.length;i++){
            if(nums[i] != 0){
                //若发生交换，这里的nums[j]必然是0，因为j右边的0肯定已经被i先前交换到j左边去了，若不是0这里i==j
                //所以是不存在将非0元素又交换到j右边的位置的情况的
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j++] = temp;
            }
        }
    }
}

剑指 Offer 21. 调整数组顺序使奇数位于偶数前面 - 力扣（Leetcode）

一道简单题，使用双指针

class Solution {
    public int[] exchange(int[] nums) {
        int[] res = new int[nums.length];
        int pre = 0;
        int tail = nums.length - 1;
        for(int i = 0; i < nums.length; i++){
            if(nums[i] % 2 == 1){
                res[pre++] = nums[i];
            }else{
                res[tail--] = nums[i];
            }
        }
        return res;
    }
}

动态规划

70. 爬楼梯 - 力扣（Leetcode）

兜兜转转又回到最初的爬楼梯… （注意声明数组为n+1）

class Solution {
    public int climbStairs(int n) {
        //这里的判断可以不要，因为测试用例里面没有0的情况
        if(n == 0){
            return 1;
        }
        int[] dp = new  int[n + 1];
        dp[0] = 1;//依据题意改的
        dp[1] = 1;
        for(int i = 2; i <= n; i++){
            dp[i] = dp[i-1] + dp[i - 2];
        }
        return dp[n];
    }
}


//have main
public class climbStairs {
    public static int climbStairs(int n) {
        //当台阶为0时，返回0还是1 得看具体测试用例的情况
        if (n <= 2) return n;
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int ans = climbStairs(n);
        System.out.println(ans);
    }
}

剑指 Offer 10- II. 青蛙跳台阶问题 - 力扣（Leetcode）题目是一样的，不同的是测试数据会大很多，需要根据题意来取模

class Solution {
    public int numWays(int n) {
        if(n == 0){
            return 1;
        }
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2;i <= n;i++){
            dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007;
        }
        return dp[n];
    }
}

剑指 Offer 10- I. 斐波那契数列 - 力扣（Leetcode）斐波那契数列的题，和上面的是一样的

class Solution {
    public int fib(int n) {
        if(n == 0){
            return 0;
        }
        int[] dp =  new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for(int i = 2;i <= n; i++){
            dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007;
        }
        return dp[n];
    }
}

338. 比特位计数 - 力扣（Leetcode）

题意：给你一个十进制数字，找出这个数字的二进制数字里面有几个1

方法一：使用Java自带的Integer.bitCount()函数，可以直接找出有多少个1

class Solution {
    public int[] countBits(int n) {
        int[] ans = new int[n + 1];
        for(int i = 1; i <= n; i++){
            ans[i] = Integer.bitCount(i); 
        }
        return ans;
    }
}

方法二：这个方法比较巧妙，首先需要找到规律

奇数：二进制表示中，奇数一定比前面那个偶数多一个 1，因为多的就是最低位的 1。

举例： 
         0 = 0       1 = 1
         2 = 10      3 = 11

偶数：二进制表示中，偶数中 1 的个数一定和除以 2 之后的那个数一样多。因为最低位是 0，除以 2 就是右移一位，也就是把那个 0 抹掉而已，所以 1 的个数是不变的。

举例：
          2 = 10       4 = 100       8 = 1000
          3 = 11       6 = 110       12 = 1100

class Solution {
    public int[] countBits(int n) {
        int[] ans = new int[n + 1];
        for(int i = 1; i <= n; i++){
            if(i % 2 == 1){
                ans[i] = ans[i - 1] + 1;
            }else{
                ans[i] = ans[i / 2];
            }
        }
        return ans;
    }
}

461. 汉明距离 - 力扣（Leetcode）和上面的题有类似的地方，都用到了Integer.bitCount()函数

题意：简单的来说，汉明距离就是这两个数字的二进制数有几位不同，遇到不同，我们就可以使用异或来解决，因为不同数字异或的结果是1，因此再搭配上Integer.bitCount()函数就可以得到答案

class Solution {
    public int hammingDistance(int x, int y) {
        return Integer.bitCount(x ^ y);
    }
}

一个类似的题

剑指 Offer 15. 二进制中1的个数 - 力扣（Leetcode）

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        return Integer.bitCount(n);
    }
}

128. 最长连续序列 - 力扣（Leetcode）

题意：就是找出数字连续的最长的序列（注意这里题意不要求序列元素在原数组中连续，因此和下面的寻找最长递增子序列是不同的，下面的寻找最长递增子序列不可以用这种排序后再dp的方法）

思路：本来想使用map试试，但是map的键用keySet()取出后，set无法使用get方法取出值，因此使用排序后用dp

class Solution {
    //排序后用dp
    public int longestConsecutive(int[] nums) {
        int len = nums.length;
        //考虑特殊情况
        if(len == 0){
            return 0;
        }
        Arrays.sort(nums);
        int res = 1;//即使是一个元素，也可以是一个连续的元素
        int[] dp = new int[len];
        dp[0] = 1;
        for(int cur = 1;cur < len;cur++){
            if(nums[cur] == nums[cur-1] + 1){
                dp[cur] = dp[cur - 1] + 1;
                res = Math.max(res,dp[cur]);//有递增的就加1
            }else if(nums[cur] == nums[cur-1]){
                dp[cur] = dp[cur - 1];//相同不变
            }else{
                 dp[cur] = 1;//否则重新计数
            }
        }
        return res;
    }
}

//have main
public class longestConsecutive {
    public int longestConsecutive(int[] nums) {
        int len = nums.length;
        //考虑特殊情况
        if(len == 0){
            return 0;
        }
        Arrays.sort(nums);
        int res = 1;//即使是一个元素，也可以是一个连续的元素
        int[] dp = new int[len];
        dp[0] = 1;
        for(int cur = 1;cur < len;cur++){
            if(nums[cur] == nums[cur-1] + 1){
                dp[cur] = dp[cur - 1] + 1;
                res = Math.max(res,dp[cur]);//有递增的就加1
            }else if(nums[cur] == nums[cur-1]){
                dp[cur] = dp[cur - 1];//相同不变
            }else{
                dp[cur] = 1;//否则重新计数
            }
        }
        return res;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int len = sc.nextInt();
        int[] nums = new int[len];
        for (int i = 0; i < len; i++) {
            nums[i] = sc.nextInt();
        }
        longestConsecutive solution = new longestConsecutive();
        int result = solution.longestConsecutive(nums);
        System.out.println(result);
    }
}

53. 最大子数组和 - 力扣（Leetcode）这道题第一次遇到是在我们团队的招新考试上，基本上算是我的动态规划的启蒙题了，我觉得很好的体现了动态规划的思想和思路，下面的这个题解我觉得比我自己写的话好很多，详细解释了动规的思想和后效性，也相当于带你入门动态规划了53. 最大子数组和题解,这个题解是真的好

class Solution {
    //一眼动规
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int max = nums[0];
        
        for(int i = 1;i<nums.length;i++){
            if(dp[i-1]>0){//注意一下这里是dp[i-1]
                dp[i] = dp[i-1]+nums[i];
                max = Math.max(dp[i],max);//在dp过程中就在找最大的值
            }else{
                dp[i] = nums[i];
                max = Math.max(dp[i],max);
            }
            
        }
        return max;
    }
}

优化空间后的

public int maxSubArray(int[] nums) {
    int pre = 0;
    int res = nums[0];
    for (int num : nums) {
        //简直是绝妙的解法
        pre = Math.max(pre + num, num);
        res = Math.max(res, pre);
    }
    return res;
}

152. 乘积最大子数组 - 力扣（Leetcode）

题意：依旧是找连续子数组中乘积最大的

思路：乘法和加法不同，乘法中因为负负得正，所以连续子数组乘积最小的值，就有可能变成最大的。因此，我们使用两个动态规划，同时维护两个值，一个是当前子数组乘积最大值，一个是乘积最小值。当遇到负数的时候，就把维护的最大值和最小值交换，之前维护的最大值因为乘上了负数，变成了最小值，同理之前的最小值也变成了最大值。参考题解：152. 乘积最大子数组 - 力扣（Leetcode）

//优化空间后的
class Solution {
    public int maxProduct(int[] nums) {
        int max = nums[0],imax = nums[0], imin = nums[0];
        for(int i = 1;i < nums.length;i++){
            if(nums[i] < 0){
                int temp = imax;
                imax = imin;
                imin = temp;
            }
            //维护的最大值
            imax = Math.max(imax * nums[i],nums[i]);
            //维护的最小值
            imin = Math.min(imin * nums[i],nums[i]);
            //寻找最终的答案
            max = max > imax ? max : imax;  
        }
        return max;
    }
}

//维护dp数组的
class Solution {
    public int maxProduct(int[] nums) {
        int length = nums.length;
        int[] dpmax = new int[length];
        int[] dpmin = new int[length];
        int max = nums[0];
        dpmax[0] = nums[0];
        dpmin[0] = nums[0];
        
        for (int i = 1; i < length; ++i) {
            //分别维护以当前位置结尾的子数组最大乘积和最小乘积
            //因为最小的可能变成最大的。所以需要三个结果里面取，用以维护最大值和最小值
            dpmax[i] = Math.max(dpmax[i - 1] * nums[i], Math.max(nums[i], dpmin[i - 1] * nums[i]));
            dpmin[i] = Math.min(dpmin[i - 1] * nums[i], Math.min(nums[i], dpmax[i - 1] * nums[i]));

            max = Math.max(max, dpmax[i]);
        }
        
        return max;
    }
}

//have main
public class maxProduct {
    public static int maxProduct(int[] nums) {
        int max = nums[0];
        int min = nums[0];
        int res = nums[0];
        for (int i = 1; i < nums.length; i++) {
            int a = nums[i] * max;
            int b = nums[i] * min;
            //max和min也同时起了dp[i - 1]功能
            max = Math.max(Math.max(a, b), nums[i]);
            min = Math.min(Math.min(a, b), nums[i]);
            res = Math.max(res, max);
        }
        return res;
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] nums = new int[n];
        for (int i = 0; i < n; i++) {
            nums[i] = sc.nextInt();
        }
        System.out.println(maxProduct(nums));
    }
}

198. 打家劫舍 - 力扣（Leetcode）一道普通的dp题

题意：你是一个小偷，要去偷东西，不能偷相邻的两家，否则会报警，问最大偷多少

思路：使用dp，当前能偷的最大值，因为不能偷相邻的，要么是当前的前面第二家加上当前值 dp[i] = dp[i-2] + num[i],要么是前面第三家加上当前值dp[i] = dp[i-3] + num[i] ，这种循环只能从第四个开始，所以数组小于三时需要特判。

下面的代码是我自己写的，不是很优雅

class Solution {
    public int rob(int[] nums) {
        int len = nums.length;
        //特判
        if(len == 1){
            return nums[0];
        }else if(len == 2){
            return Math.max(nums[0],nums[1]);
        }else if(len == 3){
            return Math.max(nums[0] + nums[2],nums[1]);
        }
        int[] dp = new int[len];
        //前面三个只有下面这一种情况
        dp[0] = nums[0];
        dp[1] = nums[1];
        dp[2] = nums[0] + nums[2]; 
        //开始 使用递推公式推导后面的结果
        for(int i = 3;i < len;i++){
            dp[i] = Math.max(dp[i - 2],dp[i - 3]) + nums[i]; 
        }
        //最后要么是最后一个最大(偷了最后一个)，或者倒数第二个最大(没有偷最后一个)
        return Math.max(dp[len - 1],dp[len - 2]);
    }
} 

198. 打家劫舍题解 - 力扣根据题解写的优雅的代码，这个题解也相当的不错，推荐一看

public int rob(int[] nums) {
    if (nums.length == 0) {
        return 0;
    }
    // 子问题：
    // f(k) = 偷 [0..k) 房间中的最大金额

    // f(0) = 0
    // f(1) = nums[0]
    // f(k) = max{ rob(k-1), nums[k-1] + rob(k-2) }

    int N = nums.length;
    int[] dp = new int[N+1];
    dp[0] = 0;
    dp[1] = nums[0];
    for (int k = 2; k <= N; k++) {
        dp[k] = Math.max(dp[k-1], nums[k-1] + dp[k-2]);
    }
    return dp[N];
}

改写成这样或许要好理解一些

class Solution {
    public int rob(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        if (nums.length == 1) {
            return nums[0];
        }
        int N = nums.length;
        int[] dp = new int[N];
        dp[0] = nums[0];
        dp[1] = Math.max(dp[0],nums[1]);
        for (int k = 2; k < N; k++) {
            //dp = dp[k-1] 说明不偷现在的k
            //dp = dp[k-2] 说明 偷了现在个节点 再加上以前第二个节点的dp
            dp[k] = Math.max(dp[k-1], nums[k] + dp[k-2]);
        }
        return dp[N-1];
    }

}

62. 不同路径 - 力扣（Leetcode）

题意：一个m*n的棋盘，只能向下或者向右走，问你走到棋盘的右下角 一共有多少种不同的路径

思路1：排列组合

在这道题中，因为只能向下或者向右走，所以相当于走过的总路径是相同的为m+n-2,同理可以得到，向右走的步数一定是m-1,向下走的一定是n-1。因此总的路径总数就可以使用组合数来求出来，但是这里直接使用阶乘的话，数字肯定会非常大，所以这里需要化简计算，具体的化简可以看下面这个示意图

class Solution {
    public int uniquePaths(int m, int n) {
        //只跟第几行第几列有关，从m+n-2步中抽出m-1步
        long ans=1;
        for(int i=0;i<Math.min(m-1,n-1);i++){            
            ans*=m+n-2-i;
            ans/=i+1;           
        }
        return (int)ans;
    }
}

思路2：dp

边边上是只有一种到达方法，所以全部初始化为1，递推公式还是比较好懂的

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for (int i = 0; i < n; i++) dp[0][i] = 1;
        for (int i = 0; i < m; i++) dp[i][0] = 1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];  
    }
}

//优化1  
//只保留上一行和当前行，就可以直接更新 空间复杂度降为了O(2n)
class Solution {
    public int uniquePaths(int m, int n) {
        int[] pre = new int[n];
        int[] cur = new int[n];
        Arrays.fill(pre, 1);
        Arrays.fill(cur,1);
        for (int i = 1; i < m;i++){
            for (int j = 1; j < n; j++){
                cur[j] = cur[j-1] + pre[j];
            }
            pre = cur.clone();
        }
        return pre[n-1]; 
    }
}

//优化2
//把存储上一行的数据也给优化掉了，加完cur这一行数据，在下一次加的时候里面已经存储的数据就相当于上一行的数据了
//空间复杂度优化为了O(n)
class Solution {
    public int uniquePaths(int m, int n) {
        int[] cur = new int[n];
        Arrays.fill(cur,1);
        for (int i = 1; i < m;i++){
            for (int j = 1; j < n; j++){
                cur[j] += cur[j-1] ;
            }
        }
        return cur[n-1];
    }
}

//have main
public class uniquePaths {
    public static int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for(int j = 0;j < n;j++) dp[0][j] = 1;
        for(int i = 0;i < m;i++) dp[i][0] = 1;
        for(int i = 1;i < m;i++){
            for(int j = 1;j < n;j++){
                dp[i][j] = dp[i - 1][j]+ dp[i][j - 1];
            }
        }
        return dp[m-1][n-1];
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int m = sc.nextInt();
        int n = sc.nextInt();
        System.out.println(uniquePaths(m, n));
    }
}

64. 最小路径和 - 力扣（Leetcode）

虽然是一道经典的动规题。但是写的时候，还是把它给想成了dfs求解，调试半天，发现做不出来。。

题意： 经典的要求你求矩形中，左上角到右下角的最短路径，而且只能向下走，或者向右走

思路：能走到某个点，说明这个点无非下面三种状态

• 这个点在矩形中，不在边边上，说明可以由前面的节点向下或者向右走到，这时候是dp[i][j] = Math.min(dp[i - 1][j],dp[i][j - 1]) + grid[i][j];
• 这个点在左边边上，只能向下走到，这时候是dp[i][j] = dp[i - 1][j] + grid[i][j];
• 这个点在最上面那一排，只能向右走到，这时候是dp[i][j - 1] + grid[i][j];

其实和62题是一样的思路，只不过这个需要把路径上的点加起来

class Solution {
    public int minPathSum(int[][] grid) {
        int rows = grid.length ,columns = grid[0].length;
        int[][] dp = new int[rows][columns];
        dp[0][0] = grid[0][0];
        for(int i = 0;i < rows;i++){
            for(int j = 0;j < columns;j++){
                if(i == 0 && j == 0) continue;
                if(i == 0) dp[i][j] = dp[i][j - 1] + grid[i][j];
                else if(j == 0) dp[i][j] = dp[i - 1][j] + grid[i][j];
                else dp[i][j] = Math.min(dp[i - 1][j],dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[rows - 1][columns - 1];
    }
}

//have main
public class minPathSum {
    public static int minPathSum(int[][] grid) {
        int m = grid.length,n = grid[0].length;
        int[][] dp =  new int[m][n];
        //初始化第一行
        dp[0][0] = grid[0][0];
        for(int j = 1;j < n;j++) dp[0][j] = dp[0][j - 1] + grid[0][j];
        //初始化第一列
        for(int i = 1;i < m;i++) dp[i][0] = dp[i - 1][0] + grid[i][0];

        for(int i = 1;i < m;i++){
            for(int j = 1;j < n;j++){
                dp[i][j] = Math.min(dp[i - 1][j] + grid[i][j],dp[i][j - 1] + grid[i][j]);
            }
        }
        return dp[m - 1][n - 1];
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int m = sc.nextInt();
        int n = sc.nextInt();
        int[][] grid = new int[m][n];
        for (int i = 0;i < m;i++){
            for (int j = 0;j < n;j++){
                grid[i][j] = sc.nextInt();
            }
        }
        System.out.println(minPathSum(grid));
    }
}

221. 最大正方形 - 力扣（Leetcode）这还是一道动态规划的题(二维dp)，一开始还以为是岛屿，后来发现示例都通不过，仔细一想，好像并不是岛屿的问题。看了一下题解，发现还是使用动态规划解决

题意：在这个数组中使用一个正方形框出元素1，且使得这个正方形面积最大，简单来说就是使框出1的正方形最大

思路：dp[i][j]推导到dp[i+1][j+1]无非三种情况，左上角被0限制，上面被0限制或者左边被0限制，这里需要明白dp[i][j]的含义，这里指的是在以dp[i-1][j-1]为右下脚的正方形的最大边长，最后我们找到这个最大的边长后，返回面积即可。这里讲的思路还不是很清楚，因此给个连接，这个题解里面写得很清楚。221. 最大正方形 题解

class Solution {
    public int maximalSquare(char[][] matrix) {
        int r  = matrix.length;
        int c = matrix[0].length;
        int maxside = 0;
        //首先特判
        if(matrix == null || r < 1 || c < 1){
            return 0;
        }

        int[][] dp = new int[r+1][c+1];
        //开始dp
        for(int i = 0;i<r;i++){
            for(int j = 0;j<c;j++){
                if(matrix[i][j] == '1'){
                    dp[i+1][j+1] = Math.min(Math.min(dp[i][j],dp[i+1][j]),dp[i][j+1]) + 1;
                    maxside = Math.max(dp[i+1][j+1],maxside);
                }
            }
        }
        return maxside*maxside;
    }
}

最长递增子序列300. 最长递增子序列 - 力扣（Leetcode）

题意：给你一个数组，叫你求出这个数组的子数组中，最长递增的有多长，注意不可以改变顺序

思路：使用dp，这里的dp[i]的含义就是到i这里前面的最长增长子序列有多长(不一定只有一个)，和上面的那些dp不同的是，因为子序列可以从index = 0,第二个就是index = i，中间的都可以不要，因此需要两重循环来解决，不断寻找前面当前值nums[i]小的数值，然后不断求 dp[i] 和 dp[j]+1的最大值，下面是示例图，还比较好理解

class Solution {
    //学dp
    public int lengthOfLIS(int[] nums) {
        //所以递推公式是什么呢
        if(nums.length == 0) return 0;
        int[] dp = new int[nums.length];
        int res = 0;
        //全部填充为1
        Arrays.fill(dp, 1);
        for(int i = 0; i < nums.length; i++) {
            for(int j = 0; j < i; j++) {
                if(nums[j] < nums[i]) dp[i] = Math.max(dp[i], dp[j] + 1);
            }
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

139. 单词拆分 - 力扣（Leetcode）单词拆分

题意：现在有一个字符串s比如是"leetcode",现在有一个字典[“leet”,“code”]，问你字典里面的单词能不能够组成s,字典里面的单词可以任意使用不限次数

思路：使用dp[i]数组代表在这个位置上面能不能被字典里面的单词所表示，用一个长度为n+1的数组，第一位为true,其他 为false(因为第0位看作空，始终可以组合出来)，然后遍历每一个单词，看能不能成功的前缀匹配上，这里需要使用一个Java里面的函数str.startsWith(String prefix, int toffset),prefix是前缀，toffset是开始的位置，全部匹配一遍之后，直接查看dp的最后一位就可以看到是否可以组合成功了

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        int length = s.length();
        boolean[] dp = new  boolean[length + 1];
        dp[0] = true;
        for(int i = 0;i < length + 1;i++){
            if(!dp[i]){
                //不是true的说明这个长度时，字典里面的单词无法满足，从这个地方遍历没有意义
                continue;
            }
            for(String word : wordDict){
                if(word.length() + i <= length && s.startsWith(word,i)){
                    dp[word.length() + i] = true;
                }
            }
            
        }
        return dp[length];
    }
}

关于背包问题

//todo

股票系列

121. 买卖股票的最佳时机 - 力扣（Leetcode）

一道比较简单的股票题，就是求最大利润，dp都没有用，只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票

class Solution {
    public int maxProfit(int[] prices) {
        //维护一个最小的
        int minprices = prices[0];
        int maxProfit = 0;
        for(int i = 0;i < prices.length;i++){
            //更新最小值
            if(prices[i] < minprices){
                minprices = prices[i];
            }
            maxProfit = Math.max(maxProfit,prices[i] - minprices);
        }
        return maxProfit;
    }
}

309. 最佳买卖股票时机含冷冻期 - 力扣（Leetcode）多状态的动态规划

题意:通过股票的买入卖出获得收益，但是同时只能持有一只股票，未卖出的情况下不能继续买，而且你卖了一只股票后，需要冷冻一天，不能继续买，具体的解析都放在代码里了

public int maxProfit(int[] prices) {
        int days = prices.length;
        // 定义动态规划状态变量，第一维记录天数，第二维记录股票的状态
        int[][] dp= new int[days][4];

        // 初始化状态变量
        // 状态0，表示不持有股票，且没卖出，意思就是本来就不持有，没做任何买卖
        dp[0][0] = 0;
        // 状态1，表示不持有股票，原因是今天卖出了（这里因为是第0天，所以没买入，所以收益也是0）
        dp[0][1] = 0;
        // 状态2，表示持有股票，今天买入的，因为是买入，所以收入是负的，
        dp[0][2] = -1 * prices[0];
        // 状态3，表示持有股票，非今天买入，从前一天继承过来的（这里因为是第0天，所以相当于是今天买入，今天卖出）
        dp[0][3] = -1 * prices[0];

        for (int i = 1; i < days; i++) {
            // 第i天不持有且本来也不持有，那说明前一天也不持有，即使持有也卖出了，那就是0和1两种情况
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]);
            // 第i天不持有，因为今天卖出了，那收益就是今天的股票价格加上 之前累加的
            dp[i][1] = Math.max(dp[i-1][2], dp[i-1][3]) + prices[i];
            // 第i天持有，而且是今天买入（排除状态2、3），那么根据冷冻期 昨天一定没有卖出今天才能买入
            dp[i][2] = dp[i-1][0] - prices[i];
            // 第i天持有，且非今天买入, 那就是之前买入，计算之前累加的
            dp[i][3] = Math.max(dp[i-1][2], dp[i-1][3]);
        }

        //因为买卖到最后，一定是不持有的（即使亏了，卖也比不卖强），所以应该是0和1两种状态，取较大值
        return Math.max(dp[days-1][0], dp[days-1][1]);
    }

72. 编辑距离 - 力扣（LeetCode） 一道比较难的二维动规，难点主要在动规的定义(存储含义)和转移方程上(这不是废话，动规的难点不都在这两点上吗…)

题意：给你两个单词比如：horse和ros，经过最少多少次变化可以从单词1变为单词2。其中，这里面的变化包括：增加字母、删除字母以及直接变化字母三种。

思路：首先就是要搞清楚，用二维dp怎么进行定义，这里的定义的dp[i][j]代表word1的前i个字母，变换到word2的前j个字母，最短的操作次数。同时需要考虑两个单词一个字母都没有的情况，因此dp数组比单词长度都要长1个单位。

同时，状态转移方程应该是这样子搞：

• 删除操作：dp[i - 1][j]
• 增加操作：dp[i][j - 1]
• 替换操作：dp[i - 1][j - 1]

具体的题解和示例图参考这篇题解72. 编辑距离 - 题解写得很好。

class Solution {
    public int minDistance(String word1, String word2) {
        //dp[i][j]表示word1前 i 个字母 转化到 word2 前 j 个需要的最少操作数

        int n1 = word1.length()+1;
        int n2 = word2.length()+1;

        int[][] dp = new int[n1][n2];

        //dp[i][0] 给第一列赋值,删除操作，从word1的字符删除到0个字符
        for(int i=0; i<n1; i++){
            dp[i][0] = i;
        }
        
        //dp[0][j] 给第一行赋值，增加操作，从0个字符增加到word2的字符
        for(int j=0; j<n2; j++){
            dp[0][j] = j;
        }

        for(int i=1; i<n1; i++){
            for(int j=1; j<n2; j++){
                if(word1.charAt(i-1) == word2.charAt(j-1)){
                    //当字符相等，不变情况总是在最小的状态，无需与增删改情况去比较
                    dp[i][j] = dp[i-1][j-1]; //no change
                }else{
                    // 删除操作：dp[i - 1][j]
                    // 增加操作：dp[i][j - 1]
                    // 替换操作：dp[i - 1][j - 1]
                    dp[i][j] =Math.min(dp[i-1][j-1],Math.min(dp[i-1][j],dp[i][j-1]))+1; //add del edit
                }
                
                System.out.println(dp[i][j]);
            }
        }
        return dp[n1-1][n2-1];
    }
}


//have main
public class minDistance {
    public static int minDistance(String word1, String word2) {
        //dp[i][j]表示word1前 i 个字母 转化到 word2 前 j 个需要的最少操作数
        int n1 = word1.length()+1;
        int n2 = word2.length()+1;
        int[][] dp = new int[n1][n2];
        //dp[i][0] 给第一列赋值,删除操作，从word1的字符删除到0个字符
        for(int i=0; i<n1; i++){
            dp[i][0] = i;
        }
        //dp[0][j] 给第一行赋值，增加操作，从0个字符增加到word2的字符
        for(int j=0; j<n2; j++){
            dp[0][j] = j;
        }
        for(int i=1; i<n1; i++){
            for(int j=1; j<n2; j++){
                if(word1.charAt(i-1) == word2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1]; //no change
                }else{
                    dp[i][j] =Math.min(dp[i-1][j-1],Math.min(dp[i-1][j],dp[i][j-1]))+1; //add del edit
                }
//                System.out.println(dp[i][j]);
            }
        }
        return dp[n1-1][n2-1];
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String word1 = sc.nextLine();
        String word2 = sc.nextLine();
        System.out.println(minDistance(word1,word2));
    }
}

10. 正则表达式匹配 - 力扣（LeetCode）给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

• '.' 匹配任意单个字符
• '*' 匹配零个或多个前面的那一个元素

为了解决这个问题，我们需要实现一个支持 ‘.’ 和 ‘’ 的正则表达式匹配。其中，‘.’ 可以匹配任意单个字符，'’ 可以匹配零个或多个前面的元素。关键在于处理这些特殊字符的匹配情况，并确保整个字符串被完全匹配。

思路：

我们可以使用动态规划来解决这个问题。动态规划的核心思想是构建一个二维数组 dp，其中 dp[i][j] 表示字符串 s 的前 i 个字符和模式 p 的前 j 个字符是否匹配。

1. 初始化：空字符串和空模式是匹配的，因此 dp[0][0] = true。接着处理模式 p 可能匹配空字符串的情况，例如模式中的每个字符后面都有一个 ‘*’，此时可以匹配零次。
2. 状态转移：
   • 如果当前字符是 ‘*’，我们需要考虑两种情况：
     • 零次匹配：忽略 ‘*’ 及其前面的字符，即 dp[i][j] = dp[i][j-2]。
     • 一次或多次匹配：当前字符必须匹配，并且之前的字符已经匹配，即 dp[i][j] = dp[i-1][j]（前提是当前字符匹配）。
   • 如果当前字符不是 ‘*’，则直接检查当前字符是否匹配，并继承之前的匹配状态。

class Solution {
    public boolean isMatch(String s, String p) {
        int m = s.length();
        int n = p.length();
        boolean[][] dp = new boolean[m + 1][n + 1];
        dp[0][0] = true;

        // 初始化第一行，处理p可能匹配空字符串的情况
        for (int j = 1; j <= n; j++) {
            if (p.charAt(j - 1) == '*' && j >= 2) {
                dp[0][j] = dp[0][j - 2];
            }
        }

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (p.charAt(j - 1) == '*') {
                    // 处理 '*' 的情况
                    // 零次匹配
                    boolean zeroMatch = dp[i][j - 2];
                    // 一次或多次匹配
                    boolean oneOrMore = false;
                    if (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.') {
                        oneOrMore = dp[i - 1][j];
                    }
                    dp[i][j] = zeroMatch || oneOrMore;
                } else {
                    // 处理非 '*' 的情况
                    if (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.') {
                        dp[i][j] = dp[i - 1][j - 1];
                    }
                }
            }
        }

        return dp[m][n];
    }
}

二分

二分法寻找的时候，最应该注意的就是边界问题。

35. 搜索插入位置 - 力扣（LeetCode）

很经典的二分，就是题目需要的返回数据不同，下面总结了一个这类二分的模版，可以套用
class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0, right = nums.length - 1; // 注意
        while(left <= right) { // 注意
            int mid = (left + right) / 2; // 注意
            if(nums[mid] == target) { // 注意
                // 相关逻辑
            } else if(nums[mid] < target) {
                left = mid + 1; // 注意
            } else {
                right = mid - 1; // 注意
            }
        }
        // 相关返回值
        return 0;
    }
}


//下面就是套模板的代码
class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while(left <= right) {
            int mid = (left + right) / 2;
            if(nums[mid] == target) {
                return mid;
            } else if(nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return left;
    }
}

最经典的二分查找的问题704. 二分查找 - 力扣（LeetCode）

class Solution {
    public int search(int[] nums, int target) {
        //二分查找
        int left = 0,right = nums.length - 1;
        while(left <= right){
            //mid = (left + right) / 2;  这样写可能会导致溢出，下面的这种写法会好一点
            int mid = left + (right - left) / 2;
            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] > target){ 
                right = mid - 1;
            }else{
                left = mid + 1;
            }
        }
        return -1;
    }
}

33. 搜索旋转排序数组 - 力扣（Leetcode） 就是叫你找一个数字的下标，找到就返回下标，否则返回-1，不过是旋转后的，且要求算法时间复杂度为O(log n)

先使用暴力

public int search(int[] nums, int target) {
    for(int i = 0;i<nums.length;i++){
        if(target == nums[i]){
            return i;
        }
    }
    return -1;
}

是可以通过的

33. 搜索旋转排序数组 题解再来看看O(log n)的,首先想到的自然就是二分

class Solution {
    //奇怪的旋转
    public int search(int[] num, int target) {
        int left = 0;
        int right = num.length - 1;
        //使用二分法
        //注意：由于有序的一边的边界值可能等于目标值，所以判断目标值是否在有序的那边时应该加个等号
        //(在二分查找某个具体值得时候如果把握不好边界值，可以再每次查找前判断下边界值，也就是while循环里面的两个if注释)
       while(left <= right){
            // if(num[left] == target) return left;
            // if(num[right] == target) return right;
           int mid = left + (right - left) / 2; //这里是为了防止栈溢出才不写成(l+r)/2
           if(num[mid] == target) return mid;//找到了
            //左边有序
            if(num[left] <= num[mid]){
                //在左边
                if(num[left] <= target && num[mid] > target){
                    right = mid - 1;
                }else{
                    //在右边
                    left = mid + 1;
                }
            }else{//右边有序
                //在右边
                if(num[right] >= target && num[mid] < target){
                    left = mid + 1;
                }else{//在左边
                    right = mid - 1;
                }
            }
       }
       return -1;
    }
}


//have main
public class search {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while(left <= right){
            int mid = left + (right - left) / 2;
            if(nums[mid] == target) return mid;
            if(nums[left] <= nums[mid]){
                //在左边
                if(nums[left] <= target && nums[mid] > target){
                    right = mid - 1;
                }else{
                    //在右边
                    left = mid + 1;
                }
            }else{
                if(nums[right] >= target && nums[mid] < target){
                    left = mid + 1;
                }else{
                    //在右边
                    right = mid - 1;
                }
            }
        }
        return -1;
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int[] nums = new int[n];
        for(int i = 0; i < n; i++){
            nums[i] = scanner.nextInt();
        }
        int target = scanner.nextInt();
        search search = new search();
        int i = search.search(nums, target);
        System.out.println(i);
    }
}

剑指 Offer 11. 旋转数组的最小数字 - 力扣（Leetcode）

这里就是要寻找旋转后的右排序数组的第一个元素，我们将他称为旋转点

当numbers[m] > numbers[j] 的时候，旋转点在右边

当numbers[m] < numbers[j] 的时候，旋转点在左边

当相等的时候，是有一个证明j–是正确的，但我实在不想看了

详见这个题解剑指 Offer 11. 旋转数组的最小数字 - 力扣题解

class Solution {
    public int minArray(int[] numbers) {
        int i = 0,j = numbers.length - 1;
        int m;
        while(i < j){
            m = (i + j) / 2;
            if(numbers[m] > numbers[j]){
                //大于边界数字了，不可能越过旋转点
                i = m + 1;
            }else if(numbers[m] < numbers[j]){
                //这里如果减一的话可能会越过旋转点
                j = m;
            }else{
                //这里有个证明，但我不想看了
                j--;
            }
        }
        return numbers[i];
    }
}

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（Leetcode）题意就是寻找相同数字的边界

改造后的二分，即使数组中有相同的数字，仍能找到更靠左的数字target

class Solution {
    //二分
    public int[] searchRange(int[] nums, int target) {
        int l = binarySearch(nums,target);//寻找左边界
        int r = binarySearch(nums,target + 1);//找到有边界右边一个
        //使用二分找两次
        
        if(l == nums.length || nums[l] != target){
            return new int[]{-1,-1};
        }
        return new int[]{l,r - 1};
    }

    //改进版 用于返回左边界
    public int binarySearch(int[] nums, int target){
        int l = 0,r = nums.length;
        while(l < r){//注意没有等号
            int mid = l + (r - l)/2;
            if(target <= nums[mid]){
                //这里有等号 即使右边找到也不返回，而是继续找，直到返回左边的
                //用于防止5,7,7,8,8,10 两个数字相邻，也是返回左边界
               r = mid;//这里没有加一
            }else{
               l = mid + 1;;
            }
        }
       return l;
    }
}

//have main
public class searchRange {
    public int[] searchRange(int[] nums, int target) {
        int l = binarySearch(nums,target);//寻找左边界
        int r = binarySearch(nums,target + 1);//找到有边界右边一个
        //使用二分找两次

        if(l == nums.length || nums[l] != target){
            return new int[]{-1,-1};
        }
        return new int[]{l,r - 1};
    }

    //改进版 用于返回左边界
    public int binarySearch(int[] nums, int target){
        int l = 0,r = nums.length;
        while(l < r){//注意没有等号
            int mid = l + (r - l)/2;
            if(target <= nums[mid]){
                r = mid;
            }else{
                l = mid + 1;;
            }
        }
        return l;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        searchRange searchRange = new searchRange();
        int n = sc.nextInt();
        int[] nums = new int[n];
        for (int i = 0; i < n; i++) {
            nums[i] = sc.nextInt();
        }
        int target = sc.nextInt();
        int[] ints = searchRange.searchRange(nums, target);
        System.out.println(Arrays.toString(ints));
    }
}

一道查询的题240. 搜索二维矩阵 II - 力扣（Leetcode）

思路：是有序的数组，很明显就会想到使用二分的方法进行查询

public boolean searchMatrix(int[][] matrix, int target) {
    if (matrix.length == 0 || matrix[0].length == 0) {
        return false;
    }
    for (int i = 0; i < matrix.length; i++) {
        //这一行的第一个元素已经大于target了，但仍然没有找到，说明后面都没有了，返回false
        if (matrix[i][0] > target) {
            break;
        }
        //说明这一行是没有当前target元素的，直接去下一行
        if(matrix[i][matrix[i].length - 1] < target){
            continue;
        } 
        int col = binarySearch(matrix[i], target);
        if (col != -1) {
            return true;
        }
    }
    return false;
}

//二分查找
private int binarySearch(int[] nums, int target) {
    int start = 0;
    int end = nums.length - 1;
    while (start <= end) {
        //这里值得注意一下，>>>1相当于除以2
        int mid = (start + end) >>> 1;
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            start = mid + 1;
        } else {
            end = mid - 1;
        }
    }
    return -1;
}

4. 寻找两个正序数组的中位数 - 力扣（Leetcode）

先来看看暴力的解法

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        int[] newnums = new int[m + n];
        //先进行特判看看是否有哪个数组是空的
        //数组1为空
        if(m == 0){
            if(n % 2 == 0){
                return (nums2[n / 2 - 1] + nums2[n / 2]) / 2.0;
            }else{
                return nums2[n / 2];
            }
        }
        //数组2为空
        if(n == 0){
            if(m % 2 == 0){
                return (nums1[m / 2 - 1] + nums1[m / 2]) / 2.0;
            }else{
                return nums1[m / 2];
            }
        }

        int i = 0,j = 0;
        int count = 0;
        
        while(count < (m + n)){
            if(i == m){
                while(j != n){
                    newnums[count++] = nums2[j++];
                }
                break;
            }

            if(j == n){
                while(i != m){
                    newnums[count++] = nums1[i++];
                }
                break;
            }

            if(nums1[i] < nums2[j]){
                newnums[count++] =  nums1[i++];
            }else{
                newnums[count++] =  nums2[j++];
            }
        }

        
        if(count % 2 == 0){
            return (newnums[count / 2 - 1] + newnums[count / 2]) / 2.0;
        }else{
            return newnums[count / 2];
        }
    }
        

}

二分

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int n = nums1.length;
    int m = nums2.length;
    int left = (n + m + 1) / 2;
    int right = (n + m + 2) / 2;
    //将偶数和奇数的情况合并，如果是奇数，会求两次同样的 k 。
    return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;  
}
    
    private int getKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
        int len1 = end1 - start1 + 1;
        int len2 = end2 - start2 + 1;
        //让 len1 的长度小于 len2，这样就能保证如果有数组空了，一定是 len1 
        if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);
        if (len1 == 0) return nums2[start2 + k - 1];

        if (k == 1) return Math.min(nums1[start1], nums2[start2]);

        int i = start1 + Math.min(len1, k / 2) - 1;
        int j = start2 + Math.min(len2, k / 2) - 1;

        if (nums1[i] > nums2[j]) {
            return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
        }
        else {
            return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));
        }
    }

}

哈希

136. 只出现一次的数字 - 力扣（Leetcode）

题意：找出数组中只出现过一次的数字

思路：一眼哈希

//根据题解优化了一下我的代码，看着更加简洁
class Solution {
    public int singleNumber(int[] nums) {
        int len = nums.length;

        Map<Integer,Integer> map = new HashMap<>();
        for(Integer i : nums){
            int count = map.get(i) == null ? 1 : map.get(i)+1;
            map.put(i,count);
        }
        for(Integer i : map.keySet()){
            if(map.get(i) == 1){
               return i;
            }
        }
        return -1;
    }
}

异或解法

思路：异或解法：异或运算满足交换律，a^b^a=a^a^b=b,因此ans相当于nums[0]^nums[1]^nums[2]^nums[3]^nums[4]… 然后再根据交换律把相等的合并到一块儿进行异或（结果为0），然后再与只出现过一次的元素进行异或，这样最后的结果就是，只出现过一次的元素（0^任意值=任意值）

int ans = nums[0];
if (nums.length > 1) {
   for (int i = 1; i < nums.length; i++) {
      ans = ans ^ nums[i];
   }
 }
 return ans;

剑指 Offer 03. 数组中重复的数字 - 力扣（Leetcode）

class Solution {
    public int findRepeatNumber(int[] nums) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int num:nums){
            map.put(num,map.getOrDefault(num,0) + 1);
        }
        for(int num:map.keySet()){
            if(map.get(num) > 1){
                return num;
            }
        }
        return -1;
    }
}

使用set效率会高一些

class Solution {
    public int findRepeatNumber(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for(int num:nums){
            if(set.contains(num)){
                return num;
            }
            set.add(num);
        }
        return -1;
    }
}

169. 多数元素 - 力扣（Leetcode）跟上面这道题一样的 思路，甚至代码都没有怎么变

class Solution {
    public int majorityElement(int[] nums) {
        Map<Integer,Integer> map = new HashMap<>();
        for(Integer i : nums){
            int count = map.get(i) == null ? 1 : map.get(i)+1; 
            map.put(i,count);
        }
        for(Integer i: map.keySet()){
            if(map.get(i) > nums.length/2){
                return i;
            }
        }
        return -1;
    }
}

287. 寻找重复数 - 力扣（Leetcode）感觉这几个题都是差不多的，连应用哈希的方法都是差不多的，不过这一道题在上面快慢指针找出口那里有另外一种思路，可以参考参考

class Solution {
    public int findDuplicate(int[] nums) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int i = 0;i < nums.length;i++){
            //找出这个数字的映射出现了几次
            int count  = map.get(nums[i]) == null ? 1 : map.get(nums[i]) + 1;
            map.put(nums[i],count);
        }
        //找出不是1的映射就是答案
        for(int i = 0;i<nums.length;i++){
            if(map.get(nums[i]) != 1){
                return nums[i];
            }
        }
        return -1;
    }
}

搜索

剑指 Offer 04. 二维数组中的查找 - 力扣（Leetcode）

给定一个二维数组，从左往右不递减，从上往下不递减，给出一个搜索target最高效的方法

我自己的逐行搜素

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        for(int i = 0;i < matrix.length; i++){
            for(int j = 0;j < matrix[0].length;j++){
                if(matrix[i][j] == target){
                    return true;
                }
            }
        }
        return false;
    }
}

大佬的思路：将这个图翻转一下，就可以获得一个类似二叉搜索树的结构，我们在根节点设置一个标志位，当target大于标志位的时候说明target在标志位列右侧，这时可以消去标志位所在的列。当target大于标志位的时候说明target在标志位行上侧，这时可以消去标志位所在的行。来个具体题解剑指 Offer 04. 二维数组中的查找 - 力扣（Leetcode）

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        int i = matrix.length - 1, j = 0;
        while(i >= 0 && j < matrix[0].length)
        {
            if(matrix[i][j] > target) i--;//消去所在行
            else if(matrix[i][j] < target) j++;//消去所在列
            else return true;
        }
        return false;
    }
}

不成系列的方法

1. 两数之和 - 力扣（LeetCode）力扣第一题，找到相加等于target的目标值，直接暴力

//have main
public class twosum {
//    输入：nums = [2,7,11,15], target = 9
//    输出：[0,1]
//    解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
    public static int[] twoSum(int[] nums, int target) {
        int[] result = new int[2];
        for(int i = 0;i < nums.length;i++){
            for(int j = i + 1;j < nums.length;j++){
                if(nums[i] + nums[j] == target){
                    result[0] = i;
                    result[1] = j;
                    return result;
                }
            }
        }
        return result;
    }

    public static void main(String[] args) {
        //输入部分
        Scanner scanner = new Scanner(System.in);
        // 读取数组长度
        int length = scanner.nextInt();

        // 读取数组元素
        int[] nums = new int[length];
        for (int i = 0; i < length; i++) {
            nums[i] = scanner.nextInt();
        }
        // 读取目标值
        int target = scanner.nextInt();
        System.out.println(Arrays.toString(twoSum(nums,target)));
    }

}

31. 下一个排列 - 力扣（Leetcode）

我们可以将该问题形式化地描述为：给定若干个数字，将其组合为一个整数。如何将这些数字重新排列，以得到下一个更大的整数。如 123 下一个更大的数为 132。如果没有更大的整数，则输出最小的整数。

思路：

• 首先从后向前查找第一个顺序对(i,i+1)，满足 a[i]<a[i+1]。这样「较小数」即为a[i]。此时 [i+1,n) 必然是下降序列。
• 如果找到了顺序对，那么在区间 [i+1,n) 中从后向前查找第一个元素j 满足 a[i]<a[j]。这样「较大数」即为 a[j]。
• 交换a[i] 与 a[j]，此时可以证明区间[i+1,n) 必为降序。我们可以直接使用双指针反转区间 [i+1,n) 使其变为升序，而无需对该区间进行排序。

直接的思路有点抽象，还是看图比较直观包含题解的图

public void nextPermutation(int[] nums) {
    //i ：小数  k ：大数
    int n = nums.length, i = n - 1, j = i, k = n - 1;
    //从后向前找到第一个相邻升序的元素对
    while(i > 0 && nums[i] <= nums[i - 1]){
        i--;
    }
    //没进if说明已经是最大排列了，直接整个倒过来
    if(i > 0){
        //找到i-1后续中第一个大于nums[i-1]的数
        while(j > i && nums[j] <= nums[i - 1]){
            j--;
        }
        //交换
        int temp = nums[i - 1];
        nums[i - 1] = nums[j];
        nums[j] = temp;
    }

    //将i后面的数变为升序
    while(i < k){
        int temp = nums[i];
        nums[i++] = nums[k];
        nums[k--] = temp;
    }
}

//have main
public class nextPermutation {
    public static void nextPermutation(int[] nums) {
        int n = nums.length, i = n - 1, j = i, k = n - 1;
        while(i > 0 && nums[i] <= nums[i - 1]){
            i--;
        }
        if(i > 0){
            while(j > i && nums[j] <= nums[i - 1]){
                j--;
            }
            int temp = nums[i - 1];
            nums[i - 1] = nums[j];
            nums[j] = temp;
        }
        while(i < k){
            int temp = nums[i];
            nums[i++] = nums[k];
            nums[k--] = temp;
        }
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] nums = new int[n];
        for(int i = 0; i < n; i++){
            nums[i] = sc.nextInt();
        }
        nextPermutation(nums);
        for(int i = 0; i < n; i++){
            System.out.print(nums[i] + " ");
        }
    }
}

48. 旋转图像 - 力扣（Leetcode）旋转图像

思路：虽然题目要求需要原地旋转，但是是可以使用辅助数组的

参考题解：48. 旋转图像 题解

//辅助矩阵
class Solution {
    public void rotate(int[][] matrix) {
        int[][] newMatrix = new int[matrix.length][matrix[0].length];
        for(int i = 0;i < matrix.length;i++){
            for(int j = 0;j < matrix[0].length;j++){
                newMatrix[j][matrix[0].length - i -1] = matrix[i][j];
            }
        }
        for(int i = 0;i < matrix.length;i++){
            for(int j = 0;j < matrix[0].length;j++){
                 matrix[i][j] = newMatrix[i][j];
            }
        }
    }
}

//原地修改
class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix[0].length;
        for(int i = 0;i < n/2;i++){
            //奇偶有所不同
            for(int j = 0;j < (n+1)/2;j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n-1-j][i];
                matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
                matrix[n-1-i][n-1-j] = matrix[j][n-1-i];
                matrix[j][n-1-i] = temp;
            }
        }

    }
}

//have main
public class rotate {
    public void rotate(int[][] matrix) {
        int n = matrix[0].length;
        for(int i = 0;i < n/2;i++){
            //奇偶有所不同
            for(int j = 0;j < (n+1)/2;j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n-1-j][i];
                matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
                matrix[n-1-i][n-1-j] = matrix[j][n-1-i];
                matrix[j][n-1-i] = temp;
            }
        }
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[][] matrix = new int[n][n];
        for(int i = 0;i < n;i++){
            for(int j = 0;j < n;j++){
                matrix[i][j] = sc.nextInt();
            }
        }

        rotate r = new rotate();
        r.rotate(matrix);
        System.out.print("[");
        for(int i = 0;i < n;i++){
            System.out.print(Arrays.toString(matrix[i]) + " ");
        }
        System.out.print("]");
    }
}

49. 字母异位词分组 - 力扣（Leetcode）

题意：找出字母一样但是顺序不一样的单词

思路：每个单词的字母都是一样的，那么使用排序后，字母的顺序也一定是一样的，将其作为key，然后在map里面使用ArrayList存上所有这个单词的异型单词

class Solution {
    //寻找字母一样的单词？

    //一样的字母，排序后是一样的，就可以作为哈希表的键
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String,List<String>> map =  new HashMap<>();
        for(String s:strs){
            char[] array = s.toCharArray();//先转换为数组
            Arrays.sort(array);//没有返回值
            String key = new String(array);//排序后再转换为字符串
            //类似拉链法
            List<String> list = map.getOrDefault(key,new ArrayList<String>());
            //这个函数是返回key，或是返回一个默认值，这里不能直接使用get，否则后面可能会空指针异常
            list.add(s);
            map.put(key,list);
        }
        return  new ArrayList<List<String>>(map.values());
    }
}

//have main
public class groupAnagrams {
    public static List<List<String>> groupAnagrams(String[] strs) {
        Map<String,List<String>> map = new HashMap<>();
        for(String str:strs){
            char[] array =  str.toCharArray();
            Arrays.sort(array);//没有返回值
            String key = Arrays.toString(array);
            List<String> list = map.getOrDefault(key,new ArrayList<>());
            list.add(str);
            map.put(key,list);
        }
        return new ArrayList<List<String>>(map.values());
    }

    public static void main(String[] args) {
        //eat tea tan ate nat bat
        //[["bat"],["nat","tan"],["ate","eat","tea"]]
        Scanner scanner = new Scanner(System.in);
        System.out.println("请输入一组字符串，用空格分隔:");
        String input = scanner.nextLine();
        String[] strs = input.split(" ");

        System.out.println(groupAnagrams.groupAnagrams(strs));

        scanner.close();
    }
}

55. 跳跃游戏 - 力扣（Leetcode）

题意：一个数组里的数字代表，能够跳跃的最远距离，问能不能跳到最后

思路：注意是能够跳跃的最远距离，也就是说是可以跳到比他小的距离的，那也就是说，能够跳到某一个地方，那就能到达他左边的所有地方

public boolean canJump(int[] nums) {
    //奇奇怪怪，完全不知道使用什么方法
    //只要不是0 就可以继续往前面跳
    //动规？

    int cover = 0;
    for(int i = 0;i <= cover;i++){
        //i <= cover 每次只循环到能跳到的额范围
        cover = Math.max(i + nums[i],cover);
        //i + nums[i] 是当前下标加上跳最远距离，代表现在能覆盖的最大值
        if(cover >= nums.length - 1){
            //能覆盖的范围大于数组最大下标，说明能覆盖完，可以跳到终点
            return true;
        }
    }
    return false;
}

//have main
public class canJump {
    public static boolean canJump(int[] nums) {
        int cover = 0;
        for(int i = 0;i <= cover;i++){
            cover = Math.max(i+nums[i],cover);
            if(cover >= nums.length - 1){
                return true;
            }
        }
        return false;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] nums = new int[n];
        for(int i = 0;i < n;i++){
            nums[i] = sc.nextInt();
        }
        System.out.println(canJump.canJump(nums));
    }
}

56. 合并区间 - 力扣（Leetcode）

思路：按照左端点排序后，依次遍历比较结果集合中最右边的的端点值

• 当前这个数组左端点比集合中最右边的右端点大，直接加入集合，在最右边
• 否则，重合，需要将其合并，合并的方法就是比较右端点的值，把较大的右端点值作为新的右端点值更新

class Solution {
    public int[][] merge(int[][] intervals){
        if(intervals.length == 0){
            return new int[0][2];//数组为空则返回一个新的数组回去
        }
        Arrays.sort(intervals,new Comparator<int[]>() {
            public int compare(int[] interval1,int[] interval2){
                return interval1[0] - interval2[0]; //按照左端端点的升序排序
                //这里可以使用lamba简化，为了方便理解，没有简化
            }
        });


        List<int[]> merged = new ArrayList<int[]>();
        for(int i = 0;i < intervals.length;i++){
            int l = intervals[i][0],r = intervals[i][1];
            //如果为空，或者当前数组左端点大于集合最右边集合的右端点，直接加入最右边
            if(merged.isEmpty() || merged.get(merged.size() - 1)[1] < l){
                merged.add(new int[]{l,r});
            }else{
                //更新最右边的节点
                merged.get(merged.size() -1)[1] = Math.max(merged.get(merged.size() - 1)[1], r);
            }  
        }
        return merged.toArray(new int[merged.size()][]);
        //集合转换为数组，并将其填充在new的新数组中
    }
}


//have main
public class merge {
    public static int[][] merge(int[][] intervals) {
        //lamba表达式 左端点的升序排序
        Arrays.sort(intervals,(o1, o2)->{return o1[0] - o2[0];});
        List<int[]> merged = new ArrayList<>();
        for(int i = 0;i < intervals.length;i++){
            int l = intervals[i][0],r = intervals[i][1];
            if(merged.size() == 0 || l > merged.get(merged.size() - 1)[1]){
                //加入最右端
                merged.add(intervals[i]);
            }else{
                //更新最右端
                merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1],r);
            }
        }
        //传入0也可以,toArray()会自动设置merged集合的长度
        //当T泛型的长度没有list的size大时，会以size长度返回T；否则，使用传入的T。所以使用时不管写0还是其它数字，都没关系，习惯写0。
        return merged.toArray(new int[0][]);
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        //传入数组的数量
        int n = sc.nextInt();
        int[][] intervals = new int[n][2];
        for(int i = 0;i < n;i++){
            //传入数组的元素
            int l = sc.nextInt();
            int r = sc.nextInt();
            intervals[i][0] = l;
            intervals[i][1] = r;
        }

        int[][] res = merge(intervals);
        //可以直接将二维数组转换为字符串
        System.out.println(Arrays.deepToString(res));
    }
}

238. 除自身以外数组的乘积 - 力扣（Leetcode）像是dp，但是好像又不是dp

题意：由题目的名字很容易就可以看出，是求除了这个数字外的数组乘积，值得注意的是，这里题目规定了不能使用除法，并且需要使用时间复杂度为O(n)的算法,这个题解也很好，值得一看238. 除自身以外数组的乘积-题解

思路：将该数字前的数字乘积相乘，后面的数字相乘，最终再乘一次，得出最终答案。这样求左边数字乘积的时候遍历一遍，右边的时候遍历一遍，最终再遍历一遍，一共遍历三遍，成功在O(n)的复杂度下求出了结果

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int[] L = new int[nums.length];
        int[] R = new int[nums.length];
        int[] ans = new int[nums.length];
        
        //求左边的前缀乘积
        L[0] = 1;//左边没有元素，初始化为1
        for(int i = 1 ;i<nums.length;i++){
            L[i] = L[i-1] * nums[i-1];//将前一个位置的左边乘积，和前一个数字相乘就是现在位置左边的乘积
        }
        //求右边的后缀乘积
        //原理同上，需要注意的就是这里的i不要忘记还有一个=0
        R[nums.length-1] = 1;
        for(int i = nums.length-2;i>=0;i--){
            R[i] = R[i+1] * nums[i+1];
        }

        //求出最终答案
        for(int i = 0;i<nums.length;i++){
            ans[i] = L[i] * R[i];
        }

        return ans;
    }
}

优化空间复杂度：

只使用一个ans数组，先将之前的前缀乘积直接就存储到ans中，后面的后缀乘积使用变量R不断更新，同时也乘进ans数组中，这样就只使用一个数组且减少了一次循环完成了题目，因为题目说输出数组不算进空间复杂度中，因此这里的空间复杂度是O(1)

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int[] ans = new int[nums.length];
        
        //求左边的前缀乘积
        ans[0] = 1;
        for(int i = 1 ;i<nums.length;i++){
            ans[i] = ans[i-1] * nums[i-1];
        }
        //求右边的后缀乘积并同时合并到之前的前缀乘积中求出最终答案
        int R = 1;
        
        for(int i = nums.length-2;i>=0;i--){
            R = R * nums[i+1];
            ans[i] = ans[i] * R;
        }

        return ans;
    }
}

406. 根据身高重建队列 - 力扣（Leetcode）

注意：如果遇到这种数对，还涉及到排序的，根据第一个降序，第二个升序或者第一个升序，第二个降序，往往能简化结题过程。

这道题的核心的思想就是 高的是看不见低的，因此我们可以先排列好高的，后面再插入低的时候，低元素的插入不会对高元素的第二个值(也就是前面有几个人身高大等于我)造成影响，因此，我们先按照身高(第一个值)进行降序排序，然后挨个插入，而因为题目要求的是第二值代表的前面有几个人身高大等于我，因此这里的第二值我们需要按照升序排序，这样挨个插入的时候，才不会对前面已经插入的值造成影响。

class Solution {
    public int[][] reconstructQueue(int[][] people) {
        Arrays.sort(people,(x,y)->{
            if(x[0] != y[0]){
                //第一个元素降序
                return y[0] - x[0];
            }else{
                //第二个元素升序
                return x[1] - y[1];
            }
        });
        List<int[]> list = new LinkedList<>();
        for(int i = 0;i < people.length;i++){
            if(list.size() > people[i][1]){
                //插入到第people[i][1]个位置上
                list.add(people[i][1],people[i]);
            }else{
                //加到队尾
                list.add(people[i]);
            }
        }
        //转化为二维数组
        return list.toArray(new int[list.size()][]);
    }
}

448. 找到所有数组中消失的数字 - 力扣（Leetcode）一道简单题

思路：就是普通的使用哈希，没有啥特别的

class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer> list = new ArrayList<>();
        Map<Integer,Integer> map = new  HashMap<>();
        for(int i = 0;i < nums.length;i++){
            int count = map.get(nums[i]) == null ? 1 : map.get(nums[i]) + 1;
            map.put(nums[i],count);
        }
        for(int i = 1;i <= nums.length;i++){
            if(map.get(i) == null){
                list.add(i);
            }
        }
        return list;
    }
}

剑指 Offer 14- I. 剪绳子 - 力扣（Leetcode）

题意简单的来说就是将一个数字分成m段，然后将这m段的长度相乘，问最大的值是多少。

这里可以采用数学求导的方法来做，经过一系列的数学求导计算，将每段分成3是最大的，如果有余数，余数是1的时候，将前一段3和1转变为2和2乘积会更大。如果最后一段是2，最后就乘以2.

详细的证明可以参考这里剑指 Offer 14- I. 剪绳子 - 力扣（Leetcode）

class Solution {
    public int cuttingRope(int n) {
        if(n <= 3){
            return n - 1;
        }
        int a = n / 3, b = n % 3;
        if(b == 0) return (int)Math.pow(3, a);
        if(b == 1) return (int)Math.pow(3, a - 1) * 4;
        //b == 2
        return (int)Math.pow(3, a) * 2;
    }
}

剑指 Offer 14- II. 剪绳子 II - 力扣（Leetcode）

升级版，将n值扩大了

//写的时候总是会溢出，需要换成long并且在最后的答案中还是需要再取余然后再转换
class Solution {
    public int cuttingRope(int n) {
        if(n <= 3){
            return n - 1;
        }
        int a = n / 3, b = n % 3;
        int p = 1000000007;
        if(b == 0) return (int)((remainder(3, a - 1, 1000000007) * 3) % p);
        if(b == 1) return (int)((remainder(3, a - 1, 1000000007) * 4) % p);
        //b == 2
        return (int)((remainder(3, a - 1, 1000000007) * 6) % p);
    }

    private long remainder(int num, int a,int p){
        long res = 1;
        for(int i = 0; i < a; i++){
            res = (res * num) % p;
        }
        return res;
    }
}

优雅一点的

class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) 
            return n - 1;
        int b = n % 3, p = 1000000007;
        long ret = 1;
        int lineNums=n/3;           //线段被我们分成以3为大小的小线段个数
        for(int i=1;i<lineNums;i++) //从第一段线段开始验算，3的ret次方是否越界。注意是验算lineNums-1次。
            ret = 3*ret % p;
        if(b == 0) 
            return (int)(ret * 3 % p);   //刚好被3整数的，要算上前一段
        if(b == 1) 
            return (int)(ret * 4 % p);   //被3整数余1的，要算上前一段

        return (int)(ret * 6 % p);       //被3整数余2的，要算上前一段
    }
}

剑指 Offer 17. 打印从1到最大的n位数 - 力扣（Leetcode）

class Solution {
    public int[] printNumbers(int n) {
        //先生成末尾的数字
        int end = (int)Math.pow(10, n) - 1;
        int[] res = new int[end];
        for(int i = 0; i < end; i++)
            res[i] = i + 1;
        return res;
    }
}

阿里笔试第二题

题目：输入一个数组，比如[9, 9, 9, 1] ,每次只能改变各个数字的二进制数的一位，求把数组里面的数字全部变成一样最少需要多少次操作。

思路：统计数组里面的数字在二进制数的各个位上的情况，因为是二进制，所以只有两种情况0和1，如果这个位上1多，就把剩下的0改成1，这就是这一位上的最少操作数，反之，就把1改成0，后面的位亦然。总结就是把每一位上0和1中较少的次数相加，就是最终最少的次数。

/**
 * @program: code
 * @description:
 * @author: Mr.Mercury
 * @create: 2023-04-12 16:54
 **/
import java.util.Scanner;

public class alino2 {
    public static void main(String[] args) {
        int[] b = new int[32];
        int sum = 0;

        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        for (int i = 1; i <= n; i++) {
            int x = sc.nextInt();
            add(x, b);
        }
        
        //找到1和0中位数比较少的那一位，相加起来
        //因为只有0和1两种情况，所以只要1的数量大于了一半就把剩下的0改成1，这需要n - b[i]次操作次数
        //反之，就把1改成0，这需要b[i]次操作次数
        double mid = n / 2.0;
       
        for (int i = 30; i >= 0; i--) {
            if (b[i] > mid) {
                sum += n - b[i];
            } else {
                sum += b[i];
            }
        }

        System.out.println(sum);
    }

    public static void add(int x, int[] b) {
        //计算数组中用二进制表示的数字在各位上的分布情况
        for (int i = 30; i >= 0; i--) {
            int j = x >> i & 1;//右移i位然后再与1 取出二进制位
            if (j == 1) {
                b[i]++;
            }
        }
    }
}

//in  4    9 9 9 9
//out 0

//in  4    9 9 9 8
//out 1

队列

优先队列

215. 数组中的第K个最大元素 - 力扣（Leetcode）一道优先队列的经典题型，其实这道题使用暴力直接快排就可以直接AC，但是题目规定的是使用O(N),这里的快排很明显是O(logN),所以这里这不符合题意.

class Solution {
    public int findKthLargest(int[] nums, int k) {
        Arrays.sort(nums);
        // int index = nums.length - 1;
        // while(k > 0){
        //     k--;
        //     index--;
        // }
        return nums[nums.length-k];
    }
}

下面主要来看一下优先队列的做法：

PriorityQueue是一个具有优先级的无界队列，其内部基于一个优先级堆实现的。优先级队列内部的元素之间的优先级是按照元素实现的Comparable的自然顺序排序的，或者是使用构造方法中传入的Comparator接口的实现类完成的。优先队列中不允许存放null元素，如果没有传入Comparator接口的实现类，那么内部的元素必须要实现Comparable接口，否则将抛出ClassCastException，因为元素在比较时转化为Comparable进行比较。

优先队列的思路是很朴素的。由于找第 K 大元素，其实就是整个数组排序以后后半部分最小的那个元素。因此，我们可以维护一个有 K 个元素的最小堆(优先队列默认就是最小堆)：

• 如果当前堆不满，直接添加；
• 堆满的时候，如果新读到的数小于等于堆顶，肯定不是我们要找的元素，只有新遍历到的数大于堆顶的时候，才将堆顶拿出，然后放入新读到的数，进而让堆自己去调整内部结构。

import java.util.Comparator;
import java.util.PriorityQueue;

public class Solution {

    public int findKthLargest(int[] nums, int k) {
        int len = nums.length;
        // 使用一个含有 k 个元素的最小堆，PriorityQueue 底层是动态数组，为了防止数组扩容产生消耗，可以先指定数组的长度
        PriorityQueue<Integer> minHeap = new PriorityQueue<>(k, Comparator.comparingInt(a -> a));
        // Java 里没有 heapify ，因此我们逐个将前 k 个元素添加到 minHeap 里
        for (int i = 0; i < k; i++) {
            minHeap.offer(nums[i]);
        }

        for (int i = k; i < len; i++) {
            // 看一眼，不拿出，因为有可能没有必要替换
            Integer topElement = minHeap.peek();
            // 只要当前遍历的元素比堆顶元素大，堆顶弹出，遍历的元素进去
            if (nums[i] > topElement) {
                // Java 没有 replace()，所以得先 poll() 出来，然后再放回去
                minHeap.poll();
                minHeap.offer(nums[i]);
            }
        }
        return minHeap.peek();
    }
}

另一种更简单的写法，同样是优先队列

class Solution {
    public int findKthLargest(int[] nums, int k) {
        PriorityQueue<Integer> heap = new PriorityQueue<>();
        for (int num : nums) {
            heap.add(num);
            if (heap.size() > k) {
                heap.poll();
            }
        }
        return heap.peek();
    }
}

重要的是理解优先队列这个结构。后面做题估计还会用到。

果然又遇到了，347. 前 K 个高频元素 - 力扣（Leetcode），这个题一看就是需要使用优先队列来做

题意：找出数组中出现频率最高的前K个元素

思路：先使用老套路哈希遍历一遍将频率算出来，然后使用优先队列，以频率作为排序依据，把key存进去，使用长度为K的最小堆，一直维持这个最小堆，直到遍历结束，即是最终的答案

class Solution {
    //哈希加堆
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int num:nums){
            int freq = map.get(num) == null ? 1 : map.get(num)+1;
            map.put(num,freq);
        }
        //后面原来可以直接写lambda表达式
        //使用优先队列构造出关于Value的最小堆，并把key存进去
        PriorityQueue<Integer> heap = new PriorityQueue<>(k,(a,b) ->{return map.get(b) - map.get(a);});
        for(int key:map.keySet()){
            heap.add(key);
        }
        //获取最终的答案
        int[] res = new int[k];
        for(int i = 0;i<k;i++){
            res[i] = heap.poll();
        }
        return res;
    }
}

滑动窗口

滑动窗口的类题目的通用模板，主体思路和模板来自滑动窗口通用题解

/* 滑动窗口算法框架 */
public String minWindow(String s, String t) {
        Map<Character, Integer> window = new HashMap<>();
        Map<Character, Integer> need = new HashMap<>();
        for (char c : t.toCharArray()) {
            need.put(c, need.getOrDefault(c, 0) + 1);
        }
        int left = 0;
        int right = 0;
        int valid = 0;
        while (right < s.length()) {
            char c = s.charAt(right);
            right++;
            //移动right，更新窗口内的数据
            ...
            
            // 判断左侧窗⼝是否要收缩
            while (valid == need.size()) {
                //保存答案,可能是这个位置
                ...
                    
                char d = s.charAt(left);
                left++;
                //移动left，更新窗口内的数据
                ...
            }
        }
        return ...
    }

其中两处 ... 表示的更新窗口数据的地方，到时候你直接往里面填就行了。

主要的思路就是：

• 滑动窗口的右边指针一直增加，直到窗口中的字符串符合要求

• 此时，我们停止增加right指针扩大窗口，转而不断增加left指针缩小窗口，直到窗口中的字符串不再符合要求。同时每次增加left，我们都需要更新一轮结果

• 重复上述步骤，直到right到达字符串s的尽头

来看看实际的例子

76. 最小覆盖子串 - 力扣（Leetcode）

题意：给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 ""

class Solution {
    public String minWindow(String s, String t) {
        Map<Character, Integer> window = new HashMap<>();
        Map<Character, Integer> need = new HashMap<>();
        for (char c : t.toCharArray()) {
            need.put(c, need.getOrDefault(c, 0) + 1);
        }
        int left = 0;
        int right = 0;
        int valid = 0;//用来判断窗口里面的合法字符
        int start = 0, len = Integer.MAX_VALUE;
        while (right < s.length()) {
            //不断扩大右边的指针
            char c = s.charAt(right);
            right++;
            if (need.containsKey(c)) {
                window.put(c, window.getOrDefault(c, 0) + 1);
                //这里需要使用equals方法，使用==的话，超过128会报错
                if (window.get(c).equals(need.get(c))) {
                    valid++;
                }
            }
            // 判断左侧窗⼝是否要收缩
            while (valid == need.size()) {
                // 不断缩小更新最小的覆盖子串
                if (right - left < len) {
                    start  = left;
                    len = right - left;
                }
                char d = s.charAt(left);
                left++;
                //移动left
                if (need.containsKey(d)) {
                    if (window.get(d).equals(need.get(d))) {
                        valid--;
                    }
                    window.put(d, window.get(d) - 1);
                }
            }
        }
        return len == Integer.MAX_VALUE ? "" : s.substring(start,start + len);
    }
}

438. 找到字符串中所有字母异位词 - 力扣（Leetcode）

题意：给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。说白了就是找到母字符串里，所有子字符串的所有排列，并返回其实索引

 class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        Map<Character,Integer> window = new HashMap<>();
        Map<Character,Integer> need = new HashMap<>();
        for(Character c : p.toCharArray()){
            need.put(c, need.getOrDefault(c, 0) + 1);
        }
        //定义左右指针
        int left = 0;
        int right = 0;
        //判断窗口内部的合法字符有多少个
        int valid = 0;
        //存储结果
        List<Integer> res = new ArrayList<>();
        while(right < s.length()){
            //向右移动窗口
            Character c = s.charAt(right);
            right++;
            if(need.containsKey(c)){
                window.put(c, window.getOrDefault(c, 0) + 1);
                //这里需要用equals方法，不然超过128的话会报错
                if(window.get(c).equals(need.get(c))){
                    valid++;
                }
            }

            //判断是否左指针移动收缩窗口
            while(right - left >= p.length()){
                //窗口内的合法字符等于需要的字符,保存起始索引
                if(valid == need.size()){
                    res.add(left);
                }
                Character d = s.charAt(left);
                left++;
                if(need.containsKey(d)){
                    if(window.get(d).equals(need.get(d))){
                        valid--;
                    }
                    window.put(d, window.get(d) - 1);
                }
            }
        }
        return res;     
    }  
}

3. 无重复字符的最长子串 - 力扣（Leetcode）

思路：这道题使用新的思路解决，滑动窗口

思路：

• 定义一个map数据结构，其中key为字符，value为字符位置加1，表示从字符位置后一个才开始不重复
• 每次都移动一次end，如果遇到和前面重复的字符就更新start的位置，也就是key的下一个位置，不断重复，直到最后

3. 无重复字符的最长子串 - 力扣（Leetcode）画解算法

class Solution {
    public int lengthOfLongestSubstring(String s) {
        int n = s.length(), ans = 0;
        Map<Character,Integer> map = new HashMap<>();
        //每次都移动end，如果遇到重复的就跳转到key的后一个位置
        for(int end = 0,start = 0;end < n;end++){
            char alpha = s.charAt(end);
            if(map.containsKey(alpha)){
                start = Math.max(map.get(alpha), start);
            }
            ans = Math.max(end - start + 1, ans);
            //更新当前end的不重复的位置
            map.put(s.charAt(end), end + 1);
        }
        return ans;
    }
}

在使用模板写一次，这里还是有一定的变化, 简化了need字符串，只要有重复的就收缩

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character, Integer> window = new HashMap<>();
        
        int left = 0;
        int right = 0;
        int res = 0;
        while (right < s.length()) {
            char c = s.charAt(right);
            right++;
            //移动right，更新窗口内的数据
            window.put(c, window.getOrDefault(c, 0) + 1);
            
            // 判断左侧窗⼝是否要收缩 有重复了(>1)就缩小左边
            while (window.get(c) > 1) {              
                char d = s.charAt(left);
                left++;
                //移动left，更新窗口内的数据
                window.put(d, window.get(d) - 1);
            }
            //因为需要不重复，所以需要左边收缩完成后，窗口里面没有重复的数据后再更新数据
            res = Math.max(res,right - left);
        }
        return res;
    }
}


//have main
public class lengthOfLongestSubstring {
    public static int lengthOfLongestSubstring(String s) {
        Map<Character,Integer> window = new HashMap<>();
        int left = 0;
        int right = 0;
        int res = 0;

        while(right < s.length()){
            //扩大右边窗口
            char c = s.charAt(right);
            right++;
            window.put(c,window.getOrDefault(c,0) + 1);

            //有重复了 缩小左边窗口
            while(window.get(c) > 1){
                char d = s.charAt(left);
                left++;
                window.put(d,window.get(d) - 1);
            }
            res = Math.max(res,right -left);
        }
        return res;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        String s = scanner.next();
        System.out.println(s + " : " + lengthOfLongestSubstring(s));
    }
}

DFS

DFS回溯

注意回溯的模板

① 画出递归树，找到状态变量(回溯函数的参数)，这一步非常重要※
② 根据题意，确立结束条件
③ 找准选择列表(与函数参数相关),与第一步紧密关联※
④ 判断是否需要剪枝
⑤ 作出选择，递归调用，进入下一层
⑥ 撤销选择

main{
    dfs(...);
}

void dfs(...){
    //满足条件返回
    if(..){
        res.add(path)//添加到最终答案中
        return;
    }
    
    for(;;){
        path.add()//添加元素
        dfs()
        path.remove()//回溯
    }
}

39. 组合总和 - 力扣（Leetcode）感觉蛮经典的一个DFS，题意是可以无限次的使用规定的数组，使他们加起来和等于target，问一共有几种组合

思路：使用DFS不断回溯，每次减去一个数组里面的数，直到最后等于0或者小于0，其中等于0走过的路径就是我们需要的组合。就如下图所示

但是有一个问题就是，这中间走过的路径是会重复的比如 [2,2,3] 和 [3,2,2]，为了解决这个问题，可以想到set事后去重，但是好像有点难搞，我们可以在遍历的时候就去重，如下图所示，后面每次的走的时候就不去走前面的数组就行，这里可以使用一个begin来实现。

class Solution {
    //找出和为target的所有组合
    //搜索回溯 dfs
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();

        //特值判断
        if(len == 0){
            return res;
        }

        //双端队列 用来存储经过的路径
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates,0,len,target,path,res);
        return res;
    }

    public void dfs(int[] candidates,int begin,int len,int target,Deque<Integer> path,List<List<Integer>> res){
        if(target < 0){
            //说明不是刚好等于target，舍弃
            return ;
        }

        if(target == 0){
            res.add(new ArrayList(path));
            return ;
        }
        //注意这里的begin是为了去重
        for(int i = begin;i<len;i++){
            //往下走一步
            path.add(candidates[i]);

            dfs(candidates,i,len,target - candidates[i],path,res);
            //回溯
            path.removeLast();
        }

    }
}

//have main
public class combinationSum {
    public static List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        Deque<Integer> path = new ArrayDeque<>();
        //特值判断
        if(candidates.length == 0){
            return res;
        }
        dfs(0,candidates,target,path,res);
        return res;
    }

    public static void dfs(int begin,int[] candidates,int target,Deque<Integer> path,List<List<Integer>> res){
        //出口
        if(target < 0){
            return;
        }
        if(target == 0){
            //可以直接添加进去
            res.add(new ArrayList(path));
            return;
        }

        for(int i = begin;i < candidates.length;i++){
            path.add(candidates[i]);
            dfs(i,candidates,target-candidates[i],path,res);
            path.removeLast();
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int len = scanner.nextInt();
        int[] candidates = new int[len];
        for(int i=0;i<len;i++){
            candidates[i] = scanner.nextInt();
        }
        int target = scanner.nextInt();
        List<List<Integer>> res = combinationSum(candidates,target);
        System.out.println(res);
    }

}

全排列

46. 全排列 - 力扣（Leetcode）

题意：找出数组里面数字的全部排列组合，一眼丁真鉴定为dfs

思路：因为全排列的数字顺序不同也可以看作一个答案，所以这里采用的是used数组来判定是否使用过该元素，且原数组没有重复元素，所以不需要剪枝

class Solution {
    //dfs
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        Deque<Integer> path = new ArrayDeque<>();
        int length = 0;//用来记录现在排列了几个了
        int[] used = new int[nums.length];//记录现在那几个元素是使用了的
        dfs(nums,res,path,0,used);
        return res;
    }

    public void dfs(int[] nums,List<List<Integer>> res,Deque<Integer> path,int length,int[] used){
        if(length >= nums.length){
            res.add(new ArrayList(path));//已经全部排列好了，返回结果
            return;
        }
        for(int i = 0;i<nums.length;i++){
            if(used[i] != 1){//如果不用这个会导致多出例如[1,1,1] [1,1,2]这样的重复数字结果
                path.add(nums[i]);
                used[i]++;
                dfs(nums,res,path,length+1,used);//继续dfs
                used[i] = 0;//回溯
                path.removeLast();//回溯
            }    
        }
        
    }
}

//have main
 public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>>  res = new ArrayList<>();
        Deque<Integer> path =  new ArrayDeque<>();
        int[] used = new int[nums.length];
        dfs(res,path,nums,nums.length,used);
        return res;
    }

    public void dfs(List<List<Integer>> res,Deque<Integer> path,int[] nums,int length,int[] used){
        if(path.size() == length){
            res.add(new ArrayList(path));
            return;
        }

        for(int i = 0;i < nums.length;i++){
            if(used[i] != 1){
                path.add(nums[i]);
                used[i] = 1;
                dfs(res,path,nums,length,used);
                used[i] = 0;
                path.removeLast();
            }
        }
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] nums = new int[n];
        for(int i = 0;i < n;i++){
            nums[i] = sc.nextInt();
        }
        permute p = new permute();
        List<List<Integer>> lists = p.permute(nums);

        System.out.print("[");
        for(int i = 0;i < lists.size();i++){
            System.out.print(Arrays.toString(lists.get(i).toArray()) + " ");
        }
        System.out.print("]");

    }

子集78. 子集 - 力扣（Leetcode）

鉴定为回溯，这里再贴一个很好的题解78. 子集 - 力扣题解

题意：找出一个数组里的所有子集

思路：这里依然使用的是start,因为题中说数组里没有重复的元素，所以没有剪枝

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        Deque<Integer> path = new ArrayDeque<>();
        List<List<Integer>> res  = new ArrayList<>();
        int start = 0;//不能重合的时候需要start来保证每次不遍历之前已经遍历过的数
        dfs(res,path,nums,start);
        return res;
    }

    public void dfs(List<List<Integer>> res,Deque<Integer> path,int[] nums,int start){
        if(path.size() > nums.length){
            return ;
        }
        res.add(new ArrayList(path));
        for(int i = start;i < nums.length;i++){
            path.add(nums[i]);
            dfs(res,path,nums,i+1);
            path.removeLast();
        }
    }
}

//have main
public class subsets {
    public static List<List<Integer>> subsets(int[] nums) {
        Deque<Integer> path = new ArrayDeque<>();
        List<List<Integer>> res = new ArrayList<>();
        dfs(nums, 0, path, res);
        return res;
    }

    public static void dfs(int[] nums, int start, Deque<Integer> path, List<List<Integer>> res) {
        if(path.size() >= nums.length){
            return ;
        }
        res.add(new ArrayList<>(path));
        for (int i = start; i < nums.length; i++) {
            path.addLast(nums[i]);
            dfs(nums, i + 1, path, res);
            path.removeLast();
        }
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int len = sc.nextInt();
        int[] nums = new int[len];
        for (int i = 0; i < len; i++) {
            nums[i] = sc.nextInt();
        }
        List<List<Integer>> result = subsets(nums);
        System.out.println(result);
    }
}

79. 单词搜索 - 力扣（Leetcode）这道题和普通的回溯有一点点的差别，这里的有四个方向，而且不用加入数组啥的

class Solution {
    //回溯
    public boolean exist(char[][] board, String word) {
        int[][] check = new int[board.length][board[0].length];
        int pathLength = 0;
        //记住这里还需要遍历一遍
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                boolean flag = dfs(board, pathLength, word,i, j, check);
                if (flag) {
                    return true;
                }
            }
        }
        return false;
    }

    public boolean dfs(char[][] board,int pathLength ,String word,int rows,int column,int[][] check){
        if(board[rows][column] != word.charAt(pathLength)){
            return false;
        }else if(pathLength == word.length()-1){
            return true;
        }
        check[rows][column] = 1;//标记为已经走过
        //这里是写在dfs外面的，写在里面的话，会导致第一个,也就是board[0][0]未被标记，导致答案错误
        int[][] direction = {{-1,0},{1,0},{0,-1},{0,1}};
        boolean flag = false;
        for(int i = 0;i < 4;i++){        
            rows += direction[i][0];
            column += direction[i][1];
            if(rows>=0 && rows<=board.length - 1 && column >= 0 && column <= board[0].length - 1 && check[rows][column] == 0){
                //没被遍历过,且没在边界
                flag = dfs(board,pathLength + 1,word,rows,column,check);
                if(flag){
                    break;
                }
              
            }
            //回溯
            rows -= direction[i][0];
            column -= direction[i][1];
        }
        //回溯
        check[rows][column] = 0;
        return flag;
    }
}

剑指offer上一样的题剑指 Offer 12. 矩阵中的路径 - 力扣（Leetcode）

class Solution {
    public boolean exist(char[][] board, String word) {
        int m = board.length;
        int n = board[0].length;
        int[][] visited = new int[m][n]; // 标记是否访问

        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(recur(board, word, i, j, 0, visited)){
                    return true;
                }
            }
        }

        return false;

    }

    private boolean recur(char[][] board, String word, int i, int j, int k, int[][] visited){
        if(i < 0 || i >= board.length || j < 0 || j >= board[0].length){
            return false;
        }

        if(visited[i][j] == 1){ // 如果之前已经访问过，则直接返回，防止递归到已经访问过的节点
            return false;
        }

        if(board[i][j] != word.charAt(k)){
            return false;
        }

        if(k == word.length()-1){ // 表示字符串已经遍历完毕，返回true
            return true;
        }

        visited[i][j] = 1; // 做选择
        // 当if(board[i][j] == word.charAt(k))满足时，开始回溯递归：
        boolean up = recur(board, word, i-1, j, k+1, visited);
        boolean down = recur(board, word, i+1, j, k+1, visited);
        boolean left = recur(board, word, i, j-1, k+1, visited);
        boolean right = recur(board, word, i, j+1, k+1, visited);

        visited[i][j] = 0; // 撤销选择

        return up || down || left || right;
    }
}

322. 零钱兑换 - 力扣（Leetcode）硬币的兑换

题意：给你一个数值，使用限定的硬币拼出来，问最少多少个

思路：一开始感觉像是回溯，试着写了以下，超出内存限制。。。

超出内存限制

class Solution {
    public int coinChange(int[] coins, int amount) {
        List<Integer> res = new ArrayList<>();
        //特值判断
        if(coins.length == 0 || amount == 0){
            return 0;
        }

        //双端队列 用来存储经过的路径
        Deque<Integer> path = new ArrayDeque<>();
        dfs(amount,coins,path,res);
        int min = Integer.MAX_VALUE;
        for(Integer size:res){
            min = Math.min(min,size);
        }
        if(min == Integer.MAX_VALUE){
            return -1;
        }
        return min;
    }

    public void dfs(int target,int[] coins,Deque<Integer> path,List<Integer> res){
        if(target < 0){
            return ;
        }
        if(target == 0){
            res.add(path.size());
            return ;
        }
        for(int i = 0;i<coins.length;i++){
            path.add(coins[i]);
            dfs(target-coins[i],coins,path,res);
            path.removeLast();
        }
    }
}

看了看题解，使用的记忆化搜索，也是使用的dfs,不过会使用一个数组每次会把已经计算过的存储起来，避免超出时间限制

public class Solution {
    public int coinChange(int[] coins, int amount) {
        if (amount < 1) {
            return 0;
        }
        return coinChange(coins, amount, new int[amount]);
    }

    private int coinChange(int[] coins, int rem, int[] count) {
        if (rem < 0) {
            return -1;
        }
        if (rem == 0) {
            return 0;
        }
        //如果已经计算过，直接返回，节约时间
        if (count[rem - 1] != 0) {
            return count[rem - 1];
        }
        int min = Integer.MAX_VALUE;
        for (int coin : coins) {
            int res = coinChange(coins, rem - coin, count);
            if (res >= 0 && res < min) {
                min = 1 + res;
            }
        }
        //将最少需要的硬币数量存储起来
        count[rem - 1] = (min == Integer.MAX_VALUE) ? -1 : min;
        return count[rem - 1];
    }
}

使用动规解决

dp[i] 表示总值i需要最少几个硬币，dp[0] = 0, dp[负数]忽略，若硬币为1,2,5那么就有

dp[1] = Min(dp[1 - 1],dp[1 - 2],dp[1 - 5]) + 1 = 1

dp[2] = Min(dp[2 - 1],dp[2 - 2],dp[2 - 5]) + 1= 1

dp[3] = Min(dp[3 - 1],dp[3 - 2],dp[3 - 5]) + 1 = 2

…

所以递推公式就已经很明显了,看代码吧

public class Solution {
    public int coinChange(int[] coins, int amount) {

        //amount可能是0，所以这里加1
        int[] dp = new int[amount+1];
        //这里使用amout+1的原因就是硬币数量可能等于amout，但是肯定不会大于，因为没有面额为负的硬币!
        Arrays.fill(dp,amount+1);
        dp[0] = 0;
        for(int i = 1;i<=amount;i++){
            for(int j = 0;j<coins.length;j++){
                if(i-coins[j]>=0){
                    dp[i] = Math.min(dp[i],dp[i-coins[j]] + 1);
                }  
            }
        }
        //前面的amount+1就是为了便于这里判断
        return dp[amount] > amount? -1 : dp[amount];
    }
}

494. 目标和 - 力扣（Leetcode）目标和

题意：给你一组数字，让你添加 + 或者是 - 号，让最终的结果等于target，问有几种方式

思路：比较笨的办法，将每一种穷尽出来，这里采用的是回溯

class Solution {
        int count = 0;
        public  int findTargetSumWays(int[] nums, int s) {
            backTrack(nums,s,0,0);
            return count;
        }

        public void backTrack(int[] nums,int s,int index,int sum){
            if(index == nums.length){
                if(sum == s){
                    count++;//记录下来
                }
                else{
                    return;
                }
            }else{
                backTrack(nums,s,index + 1,sum+nums[index]);//加的方法
                backTrack(nums,s,index + 1,sum-nums[index]);//减的方法
            }

        }
}

方法2：使用动态规划

写在动规那里了

22. 括号生成 - 力扣（Leetcode）括号生成

思路：回溯+剪枝 一开始看另外一个题解，使用动态规划，看了半天没有看懂，还是用dfs吧，这样好理解一些，这里就不同于上面那些题了，这里是需要剪枝的，因为如果左括号剩余的数量大于了右括号的数量，这就说明一定会有一个或多个左括号没有闭合(因为这里我们是从左往右挨个挨个加上去的)，因此需要把枝叶提前剪掉。

下面的高级方法没有带回溯，为了通俗易懂还是带点回溯的吧

import java.util.ArrayList;
import java.util.List;

public class Solution {

    public List<String> generateParenthesis(int n) {
        List<String> res = new ArrayList<>();
        if (n == 0) {
            return res;
        }

        StringBuilder path = new StringBuilder();
        dfs(path, n, n, res);
        return res;
    }


    /**
     * @param path  从根结点到任意结点的路径，全程只使用一份
     * @param left  左括号还有几个可以使用
     * @param right 右括号还有几个可以使用
     * @param res
     */
    private void dfs(StringBuilder path, int left, int right, List<String> res) {
        if (left == 0 && right == 0) {
            // path.toString() 生成了一个新的字符串，相当于做了一次拷贝，这里的做法等同于「力扣」第 46 题、第 39 题
            res.add(path.toString());
            return;
        }

        // 剪枝（如图，左括号可以使用的个数严格大于右括号可以使用的个数，才剪枝，注意这个细节）
        if (left > right) {
            return;
        }

        if (left > 0) {
            path.append("(");
            dfs(path, left - 1, right, res);
            path.deleteCharAt(path.length() - 1);
        }

        if (right > 0) {
            path.append(")");
            dfs(path, left, right - 1, res);
            path.deleteCharAt(path.length() - 1);
        }
    }
}

//have main
public class generateParenthesis {
    public List<String> generateParenthesis(int n) {
        List<String> res = new ArrayList<>();
        if (n == 0) {
            return res;
        }

        StringBuilder path = new StringBuilder();
        dfs(path, n, n, res);
        return res;
    }
    
    private void dfs(StringBuilder path, int left, int right, List<String> res) {
        if (left == 0 && right == 0) {
            // path.toString() 生成了一个新的字符串，相当于做了一次拷贝
            res.add(path.toString());
            return;
        }

        // 剪枝（如图，左括号可以使用的个数严格大于右括号可以使用的个数，才剪枝，注意这个细节）
        if (left > right) {
            return;
        }

        if (left > 0) {
            path.append("(");
            dfs(path, left - 1, right, res);
            path.deleteCharAt(path.length() - 1);
        }

        if (right > 0) {
            path.append(")");
            dfs(path, left, right - 1, res);
            path.deleteCharAt(path.length() - 1);
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        generateParenthesis gp = new generateParenthesis();
        List<String> res = gp.generateParenthesis(n);
        for (String s : res) {
            System.out.print(s + " ");
        }
    }
}

方法一：做减法

class Solution {
    //做减法
    public List<String> generateParenthesis(int n) {
        List<String> res = new ArrayList<>();
        if(n == 0){
            return res;
        }

        dfs("",n, n, res);
        return res;
    }

    private void dfs(String curStr, int left, int right, List<String> res){
        //括号用完了，递归结束
        //每次回退后，可以使用新的字符串变量，因此可以不用回溯
        if(left == 0 && right == 0){
            res.add(curStr);
            return;
        }
        //剪枝，减去不合理的枝叶，因为这里遍历出来的结果是不合题意或者是重复的
        if(left > right){
            return;
        }

        if(left > 0){
            dfs(curStr + "(", left - 1, right, res);
        }

        if(right > 0){
            dfs(curStr + ")", left, right - 1, res);
        }
    }
}

方法二：做加法

import java.util.ArrayList;
import java.util.List;

public class Solution {

    // 做加法

    public List<String> generateParenthesis(int n) {
        List<String> res = new ArrayList<>();
        // 特判
        if (n == 0) {
            return res;
        }

        dfs("", 0, 0, n, res);
        return res;
    }

    /**
     * @param curStr 当前递归得到的结果
     * @param left   左括号已经用了几个
     * @param right  右括号已经用了几个
     * @param n      左括号、右括号一共得用几个
     * @param res    结果集
     */
    private void dfs(String curStr, int left, int right, int n, List<String> res) {
        if (left == n && right == n) {
            res.add(curStr);
            return;
        }

        // 剪枝
        if (left < right) {
            return;
        }

        if (left < n) {
            dfs(curStr + "(", left + 1, right, n, res);
        }
        if (right < n) {
            dfs(curStr + ")", left, right + 1, n, res);
        }
    }
}

17. 电话号码的字母组合 - 力扣（LeetCode）

题意：现在有一个9键的电话按键，每个数字对应了几个字母，现在随便输入几个数字，问你一共有几种组合方式

思路：看到组合这个关键字，首先想到的就是dfs进行解题，下面就是使用通用的dfs模板写的解题方法, 除此之外，还有一个bfs的题解，一道排列的组合的题，利用类似广度优先搜索的方法，将将要入队的字母和已经在队列里面的字母组合后，然后入队，直到将数字遍历完毕

class Solution {
    public List<String> letterCombinations(String digits) {
        List<String> res = new ArrayList<>();
        if(digits.length() == 0){
            return res;
        }
        Map<Character,String> map = new HashMap<>(){{
            put('2',"abc");
            put('3',"def");
            put('4',"ghi");
            put('5',"jkl");
            put('6',"mno");
            put('7',"pqrs");
            put('8',"tuv");
            put('9',"wxyz");
        }};
        //定义一个存储路径的可变字符的变量
        Deque<Character> path = new ArrayDeque<>();
        dfs(path,map,digits,0,res);
        return res;
    }
    public void dfs(Deque<Character> path,Map<Character,String> map, String digits,int dept,List<String> res){
        //当递归到底层的时候，将路径上的参数加入结果集中 出口
        if(dept == digits.length()){
            //转换成字符串存储，并把中括号，逗号那些去除
            res.add(path.toString().replace("[","").replace("]","").replace(",","").replace(" ",""));
            return;
        }
    
        char digit = digits.charAt(dept);
        String str = map.get(digit);

        int len = str.length();
        for(int i = 0; i< len; i++){
            //将字符添加进路径结果中
            path.add(str.charAt(i));
            //递归
            dfs(path, map,digits,dept+1,res);
            //回溯
            path.removeLast();
        }
        
    }
}

//have main
//totest
public class LetterCombinations {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        //输入字符串
        String digits = scanner.nextLine();

        List<String> combinations = new LetterCombinations().letterCombinations(digits);

        System.out.println("Letter combinations:");
        for (String combination : combinations) {
            System.out.print(combination + " ");
        }

        scanner.close();
    }

    public  List<String> letterCombinations(String digits) {
        List<String> res = new ArrayList<>();
        if (digits.length() == 0) {
            return res;
        }
        Map<Character, String> map = new HashMap<Character, String>() {{
            put('2', "abc");
            put('3', "def");
            put('4', "ghi");
            put('5', "jkl");
            put('6', "mno");
            put('7', "pqrs");
            put('8', "tuv");
            put('9', "wxyz");
        }};
        Deque<Character> path = new ArrayDeque<>();
        dfs(path, map, digits, 0, res);
        return res;
    }

    private  void  dfs(Deque<Character> path, Map<Character, String> map, String digits, int dept, List<String> res) {
        if (dept == digits.length()) {
            //这个正则表达式可以匹配字符串中的[ , ]和空格这些字符。
            res.add(path.toString().replaceAll("[\\[\\], ]", ""));
            return;
        }

        char digit = digits.charAt(dept);
        String letters = map.get(digit);

        for (int i = 0; i < letters.length(); i++) {
            path.add(letters.charAt(i));
            dfs(path, map, digits, dept + 1, res);
            path.removeLast();
        }
    }
}

//bfs
class Solution {
    public List<String> letterCombinations(String digits) {
        //存储最终结果
        List<String> ans = new ArrayList<>();
        Map<Character,String[]> map = new HashMap<>();
        map.put('2',new String[]{"a","b","c"});
        map.put('3',new String[]{"d","e","f"});
        map.put('4',new String[]{"g","h","i"});
        map.put('5',new String[]{"j","k","l"});
        map.put('6',new String[]{"m","n","o"});
        map.put('7',new String[]{"p","q","r","s"});
        map.put('8',new String[]{"t","u","v"});
        map.put('9',new String[]{"w","x","y","z"});

        //存储组合结果
        Queue<String> queue = new LinkedList<>();

        for(int i = 0;i < digits.length(); i++){
            queue_letterCombinaions(queue,map.get(digits.charAt(i)));
        }

        for(String s: queue){
            ans.add(s);
        }

        return ans;
    }

    private Queue<String> queue_letterCombinaions(Queue<String> queue, String[] letters){
        if(queue.size() == 0){
            for(String letter: letters){
                queue.add(letter);
            }
        }else{
            //这里需要将现在队列的长度保存下来，不然会一直循环
            int queueLen = queue.size();
            for(int i = 0;i < queueLen; i++){
                //出队队头
                String s = queue.poll();
                //和还没有进入队列的元素组合然后入队
                for(String letter: letters){
                    queue.add(s + letter);
                }
            }         
        }
        return queue;
    }
}

岛屿问题

岛屿的问题在力扣上面是一个系列，都有一个通用的模板，可以看作是dfs的另一种题型，一般来说我们都需要遍历这些岛，而遍历这些岛无非下面这些步骤

• 查询是否走到了边界
• 查询是否是岛屿(这里使用的1是岛屿的一部分，0是海洋)
• 把这里设为已经走过
• 接着继续向四个方向走

代码示例如下

public void dfs(char[][] grid,int r,int c){
    if(!inArea(grid,r,c)){
        return;
    }

    //这个格子不是岛屿或者已经走过
    if(grid[r][c] != '1'){
        return ;
    }
    //标记为已经走过
    grid[r][c] = '2';

    //向四个方向走
    dfs(grid,r-1,c);
    dfs(grid,r+1,c);
    dfs(grid,r,c-1);
    dfs(grid,r,c+1);
}

// 判断坐标 (r, c) 是否在网格中
boolean inArea(char[][] grid, int r, int c) {
    return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
}

200. 岛屿数量 - 力扣（Leetcode）岛屿的数量

题意：找出海洋上一共有几个岛屿，相连的1且周围都是0看作一个岛屿，可以把边界都看作是0

思路：先使用dfs对每一个是1的节点遍历，如果它走出了dfs说明这个岛屿已经遍历完毕，将岛屿上面的1都标记为了2，视为已经走过，然后将结果+1即可。按这个方法，直至遍历完成。

class Solution {
    //岛屿数量
    public int numIslands(char[][] grid) {
        int res = 0;
        for(int i = 0;i < grid.length;i++){
            for(int j = 0;j < grid[0].length;j++){
                //遍历每一个1节点
                if(grid[i][j] == '1'){
                    dfs(grid,i,j);
                    res++;
                }
            }
        }
        return res;
    }
    
    public void dfs(char[][] grid,int r,int c){
        if(!inArea(grid,r,c)){
            return;
        }

        //这个格子不是岛屿或者已经走过
        if(grid[r][c] != '1'){
            return ;
        }
        //标记为已经走过
        grid[r][c] = '2';

        dfs(grid,r-1,c);
        dfs(grid,r+1,c);
        dfs(grid,r,c-1);
        dfs(grid,r,c+1);
    }

    // 判断坐标 (r, c) 是否在网格中
    boolean inArea(char[][] grid, int r, int c) {
        return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
    }

}

剑指 Offer 13. 机器人的运动范围 - 力扣（Leetcode）

题意：简单的来说就是向四个方向走，求能到达多少个地方，不过增加了一条不能进入行坐标和列坐标的数位之和大于k的格子,在判断的边界的时候，一起判断一下就好

DFS

class Solution {
    public int movingCount(int m, int n, int k) {
        boolean[][] visited = new boolean[m][n];
        return dfs(visited, m ,n ,k , 0 , 0);
    }

    private int dfs(boolean[][] visited, int m ,int n, int k, int i , int j){
        if(i >= m || j >= n || visited[i][j] || bitSum(i) + bitSum(j) > k){
            return 0;
        }
        visited[i][j] = true;
        //这里加的1相当于当前节点
        //从0 开始也只有向下和向右开始了
        return  1 + dfs(visited, m, n, k, i + 1, j) + dfs(visited, m, n, k, i, j + 1);
    }
    //计算数位之和
    private int bitSum(int num){
        int sum = 0;
        while(num > 0){
            sum += num % 10;
            num /= 10;
        }
        return sum;
    }
}

BFS

class Solution {
    public int movingCount(int m, int n, int k) {
        boolean[][] visited = new boolean[m][n];
        Deque<int[]> queue = new ArrayDeque<>();
        int res = 0;
        return bfs(visited, queue, m, n, k, res);
    }

    private int bfs(boolean[][] visited, Deque<int[]> queue, int m ,int n, int k,int res){
        //记得初始化queue;
        queue.add(new int[]{0,0});
        while(queue.size() != 0){
            int[] index = queue.poll();
            int i  = index[0];
            int j  = index[1];
            if(i >= m || j >= n || visited[i][j] || bitSum(i) + bitSum(j) > k) continue;
            visited[i][j] = true;
            res++;
            queue.add(new int[]{i + 1,j});
            queue.add(new int[]{i,j + 1});
        }
        return res;
    }

    private int bitSum(int num){
        int sum = 0;
        while(num > 0){
            sum += num % 10;
            num /= 10;
        }
        return sum;
    }
}

BFS

先看一遍树的DFS遍历

void dfs(TreeNode root) {
    if (root == null) {
        return;
    }
    dfs(root.left);
    dfs(root.right);
}

再来看看树的层序遍历，这里是使用BFS实现的

void bfs(TreeNode root) {
    Queue<TreeNode> queue = new ArrayDeque<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll(); // Java 的 pop 写作 poll()
        if (node.left != null) {
            queue.add(node.left);
        }
        if (node.right != null) {
            queue.add(node.right);
        }
    }
}

单独的一层拎出来

// 二叉树的层序遍历
void bfs(TreeNode root) {
    Queue<TreeNode> queue = new ArrayDeque<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        int n = queue.size();
        for (int i = 0; i < n; i++) { 
            // 变量 i 无实际意义，只是为了循环 n 次
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
        }
    }
}

102. 二叉树的层序遍历 - 力扣（Leetcode）

题意：这道题的层序遍历和上面并没有什么本质的区别，值得注意的就是这里返回的时候需要将每一层的数据隔一下，因此这里我们需要每次进入下一层之前，数一下队列有多长，然后进行一下循环，将每一层隔离开

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();

        Deque<TreeNode> queue = new ArrayDeque<>();
        if(root != null){
            queue.add(root);
        }
        while(!queue.isEmpty()){
            //把每一层的单独拎出来
            int n = queue.size();
            List<Integer> level = new ArrayList<>();
            for(int i = 0;i < n; i++){
                TreeNode node = queue.poll();
                level.add(node.val);
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
            res.add(level);
        }
        return res; 
    }
}

104. 二叉树的最大深度 - 力扣（Leetcode）

题意：题意如题目名，就是求二叉树的最大深度，这里提供两种思路

BFS方法和上面的题，结构没有什么太大的区别，主要就是在每次的层循环之前来个计数器就是它的深度了

class Solution {
    public int maxDepth(TreeNode root) {
        Deque<TreeNode> queue = new ArrayDeque<>();
        int depth = 0;
        if(root != null){
            queue.add(root);
        }
        while(!queue.isEmpty()){
            int size = queue.size();
            depth++;
            //每次都先处理一层，因此这里循环几次就是有多深
            //注意这里的i < size 不可以直接写i < queue.size() 因为队列的长度在变化
            for(int i = 0;i < size; i++){
                TreeNode node = queue.poll();
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
        }
        return depth;
    }
}

DFS的方法，这种方法更加的简单，更推荐这种

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        return Math.max(left,right) + 1;//加上1就是加上自己本身
    }
}

226. 翻转二叉树 - 力扣（Leetcode）

题意：把二叉树的左右对调，这里也是提供两种实现的方法

BFS，依然是通过在遍历的时候交换左右子树来实现这个功能

class Solution {
    public TreeNode invertTree(TreeNode root) {
        Deque<TreeNode> queue = new ArrayDeque<>();
        if(root != null){
            queue.add(root);
        }
        while(!queue.isEmpty()){
            TreeNode node = queue.poll();
            //交换左右子树
            TreeNode temp = node.left;
            node.left = node.right;
            node.right = temp;
            if(node.left != null){
                queue.add(node.left);
            }
            if(node.right != null){
                queue.add(node.right);
            }
        }
        return root;
    }
}

DFS，就是在普通的dfs的遍历中加入交换

class Solution {
    public TreeNode invertTree(TreeNode root) {
        dfs(root);
        return root;
    }

    private void dfs(TreeNode root){
        if(root == null){
            return;
        }
        //交换左右子树
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        dfs(root.left);
        dfs(root.right);
    }
}

剑指 Offer 27. 二叉树的镜像 - 力扣（LeetCode） 跟前面的那道题是一样的，这里采用dfs的方法来解决

class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if(root == null){
            return root;
        }
        //交换
        TreeNode temp = new TreeNode();
        temp.left = root.left;
        root.left = root.right;
        root.right = temp.left;
        mirrorTree(root.left);
        mirrorTree(root.right);
        return root;
    }
}

207. 课程表 - 力扣（Leetcode）

拓扑排序，将每个节点的入度结合起来，只有入度是0的时候才能继续向后走，具体的解析可以参考下面的题解

207. 课程表 思路

class Solution {
    // 节点的入度: 使用数组保存每个节点的入度,
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 1.课号和对应的入度
        Map<Integer, Integer> inDegree = new HashMap<>();
        // 将所有的课程先放入
        for (int i = 0; i < numCourses; i++) {
            inDegree.put(i, 0);
        }
        // 2.依赖关系, 依赖当前课程的后序课程
        Map<Integer, List<Integer>> adj = new HashMap<>();



        // 初始化入度和依赖关系
        for (int[] relate : prerequisites) {
            // (3,0), 想学3号课程要先完成0号课程, 更新3号课程的入度和0号课程的依赖(邻接表)
            int cur = relate[1];
            int next = relate[0];
            // 1.更新入度
            inDegree.put(next, inDegree.get(next) + 1);
            // 2.当前节点的邻接表
            if (!adj.containsKey(cur)) {
                adj.put(cur, new ArrayList<>());
            }
            adj.get(cur).add(next);
        }

        // 3.BFS, 将入度为0的课程放入队列, 队列中的课程就是没有先修, 可以学的课程
        Queue<Integer> q = new LinkedList<>();
        for (int key : inDegree.keySet()) {
            if (inDegree.get(key) == 0) {
                q.offer(key);
            }
        }
        // 取出一个节点, 对应学习这门课程.
        // 遍历当前邻接表, 更新其入度; 更新之后查看入度, 如果为0, 加入到队列
        while (!q.isEmpty()) {
            int cur = q.poll();
            // 遍历当前课程的邻接表, 更新后继节点的入度
            //遍历到最后一个节点，这个节点是没有后续依赖的节点的，所以直接跳过，不然会空指针异常
            if (!adj.containsKey(cur)) {
                continue;
            }
            List<Integer> successorList = adj.get(cur);

            for (int k : successorList) {
                inDegree.put(k, inDegree.get(k) - 1);
                if (inDegree.get(k) == 0) {
                    q.offer(k);
                }
            }
        }

        // 4.遍历入队, 如果还有课程的入度不为0, 返回fasle
        for (int key : inDegree.keySet()) {
            if (inDegree.get(key) != 0) {
                return false;
            }
        }
        return true;

    }
    //这里可以不要
    // public static void main(String[] args) {
    //     int[][] course = new int[][]{
    //             {3,0}, {3,1}, {4,1}, {4,2}, {5,3}, {5,4}
    //     };
    //     boolean res = new Solution().canFinish(6, course);
    //     System.out.println(res);
    // }
}

并查集

【算法与数据结构】—— 并查集_酱懵静的博客-CSDN博客_并查集这是一篇关于并查集的文章，我觉得写得很好，推荐阅读

399. 除法求值题解力扣（Leetcode再来看看这道题，这道题，是使用并查集解决的，将每个数字与根节点的倍数表达出来，然后需要求两者之间的倍数(就是除法)d额时候，就通过这个根节点的倍数除就行，这就是基本的思想。具体的实现就需要用到并查集的一些知识了，比如路径压缩,具体的代码还是挺复杂的 题解

import java.util.HashMap;
import java.util.List;
import java.util.Map;

//并查集的parent[i]指的是在位置i的元素的父节点位置在perent[i]
public class Solution {

    public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries){
        int equationsSize = equations.size();

        UnionFind unionFind = new UnionFind(2 * equationsSize);

        Map<String,Integer> map = new HashMap<>();
        int id = 0;
        for(int i = 0;i<equations.size();i++){
            String var1 = equations.get(i).get(0);
            String var2 = equations.get(i).get(1);
            //这里是反过来将map中的key作为值，把value作为键来使用的
            if(!map.containsKey(var1)){
                map.put(var1,id++);
            }

            if(!map.containsKey(var2)){
                map.put(var2,id++);
            }
            //生成并查集
            unionFind.join(map.get(var1),map.get(var2),values[i]);
    }

     // 第 2 步：做查询
        int queriesSize = queries.size();
        double[] res = new double[queriesSize];
        for (int i = 0; i < queriesSize; i++) {
            String var1 = queries.get(i).get(0);
            String var2 = queries.get(i).get(1);

            Integer id1 = map.get(var1);
            Integer id2 = map.get(var2);

            if (id1 == null || id2 == null) {
                res[i] = -1.0d;
            } else {
                res[i] = unionFind.isConnected(id1, id2);
            }
        }
        return res;
    }

    class UnionFind{
        private int[] parent;
        //权值
        private double[] weight;
        //构造函数
        public UnionFind(int n){
            this.parent = new int[n];
            this.weight = new double[n];
            for(int i = 0;i < n;i++){
                parent[i] = i;
                weight[i] = 1.0d;
            }
        }

        public void join(int x,int y,double value){
            int rootx = find(x);
            int rooty = find(y);
            if(rootx != rooty){
                //合并起来
                parent[rootx] = rooty;
            }
            //关系式的推导见下面的示意图
            weight[rootx] = weight[y] * value / weight[x];
        }

        //路径压缩
        //这里采用的是优化find函数，使用递归，一边查找一边改变并查集的结构
        public int find(int x){
            if(x != parent[x]){
                int origin = parent[x];
                parent[x] = find(parent[x]);
                //赋值权重
                weight[x] *= weight[origin];
            }
            return parent[x];
        }

        public double isConnected(int x,int y){
            int rootx = find(x);
            int rooty = find(y);
            if(rootx == rooty){
                return weight[x]/weight[y];
            }else{
                return -1.0;
            }
        }
    }
}

字符串

一个字符串，比如“dddafffffbbb” 根据字母出现的次数，从到小输出字母。如果相同就按字母acs码从大到小输出

预期结果：fdba

import java.util.HashMap;
import java.util.Map;
import java.util.Set;

public class charsort {

    public static void main(String[] args) {
        // 1. 定义一个字符串
        String s = "dddafffffbbb";
        // 3. 创建一个Map集合,用于存储字符与出现次数的关系
        Map<Character,Integer> map = new HashMap<Character, Integer>();

        for(char c : s.toCharArray()) {
            map.put(c, map.getOrDefault(c,0)+1);
        }

        Set<Character> set= map.keySet();// 获取到map集合中的所有key值

        System.out.println(set);

        while(!map.isEmpty()) {
            // 7. 通过遍历每一个key的值,获取到对应的value值
            int maxValue = 0;
            Character maxZiFu = null;
            for(Character cha : set) {
                int value= map.get(cha);
                if(value > maxValue) {// 为了将当前map集合中的最大值获取到
                    maxValue = value;
                    maxZiFu = cha;
                }else if (value == maxValue) {//如果相等按照asc码进行排序
                    maxValue = value;
                    maxZiFu = cha > maxZiFu ? cha : maxZiFu;
                }


            }

            System.out.println(maxZiFu + "==" + maxValue);
            // 8. 将最大的键值对输出之后,从map集合中删除
            map.remove(maxZiFu);
        }

    }

}

中心扩展法求回文子串

求回文子串这种题的思想就是找中心点然后向两边进行扩展，直到找到全部的回文子串，下面根据题来具体的看看

647. 回文子串 - 力扣（Leetcode）

题意就是要求你找出字符串里面有多少个回文子串，单独一个字符也算是回文子串，针对找回文子串，我们首先需要的就是找到中心点，而作为偶数或者是奇数为中心点的话是有区别的，如一个单独字符串(一个字母的)无法通过向两边扩展的方式得到形如abba的字符串，因此，最终的中心点需选用一个字符和有两个字符的作为中心点，如果再多就可以通过1个或者2个扩展得到，所以中心点有2 * len -1 个

• 为什么有 2 * len - 1 个中心点？
  aba 有5个中心点，分别是 a、b、a、ab、ba
  abba 有7个中心点，分别是 a、b、b、a、ab、bb、ba
• 什么是中心点？
  中心点即 left 指针和 right 指针初始化指向的地方，可能是一个也可能是两个
• 为什么不可能是三个或者更多？
  因为 3 个可以由 1 个扩展一次得到，4 个可以由两个扩展一次得到

具体的中心点的顺序(如 abba 作为母字符串 ) 可以由下图看出，而左右的指针满足下面的规律

• left = center / 2
• right = left + center % 2;

class Solution {
     public int countSubstrings(String s) {
        // 中心扩展法
        int ans = 0;
        for (int center = 0; center < 2 * s.length() - 1; center++) {
            
            int left = center / 2;
            int right = left + center % 2;

            while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)){
                ans++;
                left--;
                right++;
            }
        }
        return ans;
    }
}

5. 最长回文子串 - 力扣（Leetcode）最长回文子串

题意：

思路：中心扩散的方法

不断寻找可能是中心节点的子串，这里包含两种可能，子串是偶数或者是奇数，如果是偶数，就需要先向一边进行扩散，再向两边扩散

这里的left和right都是字符串两边+1的位置，并没有包含在字符串中，所以需要注意一下

5. 最长回文子串 - 力扣（Leetcode）题解

class Solution {
    public String longestPalindrome(String s) {
        if(s == null || s.length() == 0){
            return "";
        }
        int strLen = s.length();
        int left = 0;
        int right = 0;
        int len = 1;
        int maxStart = 0;
        int maxLen = 0;
        
        for(int i = 0; i < strLen; i++){
            left = i - 1;
            right = i + 1;
            //当是偶数的回文串的时候
            while(left >= 0 && s.charAt(left) == s.charAt(i)){
                len++;
                left--;
            }
            while(right < strLen && s.charAt(right) == s.charAt(i)){
                len++;
                right++;
            }
            while(left >= 0 && right < strLen && s.charAt(left) == s.charAt(right)){
                len = len + 2;
                left--;
                right++;
            }
            //保存最大值
            if(len > maxLen){
                maxLen = len;
                maxStart = left;
            }
            len = 1;
        }
        return s.substring(maxStart + 1, maxStart + 1 + maxLen);
    }
}

如果根据上面一道题的写法写的话是这样的

class Solution {
    public String longestPalindrome(String s) {
        if(s == null || s.length() == 0){
            return "";
        }
        int strLen = s.length();
        String res = "";
        
        for(int i = 0; i < strLen * 2 - 1; i++){
            int left = i / 2;
            int right = left + i % 2;
            while(left >= 0 && right < strLen && s.charAt(left) == s.charAt(right)){
                String temp = s.substring(left,right + 1);
                //保存最大值
                if(temp.length() > res.length()){
                    res = temp;
                }
                left--;
                right++;
            }
        }
        return res;
    }
}

//have main
public class longestPalindrome {
    public static String longestPalindrome(String s) {
        // 特例判断
        if (s == null || s.length() == 0) {
            return "";
        }
        int len = s.length();
        String res = "";

        // 中心拓展
        for (int center = 0; center < 2 * len - 1; center++) {
            int left = center / 2;
            int right = left + center % 2;
            while (left >= 0 && right < len && s.charAt(left) == s.charAt(right)) {
                // 保存最长的子串  substring是左闭右开[
                String substring = s.substring(left, right + 1);
                res = res.length() > substring.length() ? res : substring;
                left--;
                right++;
            }
        }

        return res;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.print("请输入一个字符串: ");
        String input = scanner.nextLine();
        System.out.println("最长回文字串为：" + longestPalindrome(input));
    }
}

再来看看dp的解法

dp解法的思想是，首先dp[l][r]为true代表字符串从下标 l - r的子串是回文的，那么可以容易知道如果下标 l 对应的字符和下标r对应的字符相等，且前一个dp数组，也就是去除了两边字符的dp[l][r]为true，那么dp[l][r]也为true，值得注意的是，这里因为需要赋初值，所以还需要增加一个条件r - l <= 2且两边的字符相等，那么也为true

public String longestPalindrome(String s) {
        if (s == null || s.length() < 2) {
            return s;
        }
        int strLen = s.length();
        int maxStart = 0;  //最长回文串的起点
        int maxEnd = 0;    //最长回文串的终点
        int maxLen = 1;  //最长回文串的长度

        boolean[][] dp = new boolean[strLen][strLen];

        for (int r = 1; r < strLen; r++) {
            for (int l = 0; l < r; l++) {
                if (s.charAt(l) == s.charAt(r) && (r - l <= 2 || dp[l + 1][r - 1])) {
                    dp[l][r] = true;
                    if (r - l + 1 > maxLen) {
                        maxLen = r - l + 1;
                        maxStart = l;
                        maxEnd = r;

                    }
                }

            }

        }
        return s.substring(maxStart, maxEnd + 1);
    }

快速幂

剑指 Offer 16. 数值的整数次方 - 力扣（Leetcode）

题意就是简单的求幂运算，直接使用Math.pow()就行，但是很明显不会这么简单，这里采用高级一点的做法，可以将时间复杂度降低到O(logn) 级别(二分)

简单的来说就是将x的n次方，转换为x的平方的n/2方。这里的n需要判断一下奇偶数，如果是奇数，就把多出来的那个x乘进去res, 偶数就不用管

具体的题解推荐剑指 Offer 16. 数值的整数次方 - 力扣题解

class Solution {
    public double myPow(double x, int n) {
        double res = 1.0;
        if(n < 0){
            n = -n;
            x = 1/x;
        }
        while(n > 0){
            if(n % 2 == 1){
                res *= x;
            }
            x *= x;
            n >>= 1; //就是向下取整
        }
        return res;
    }
}

上面的代码最后一个样例是通不过的，int 会超出限制，因此我们采用一个long 类型来暂存就可以了

class Solution {
    public double myPow(double x, int n) {
        double res = 1.0;
        long b = n;
        if(b < 0){
            b = -b;
            x = 1/x;
        }
        while(b > 0){
            if(b % 2 == 1){
                res *= x;
            }
            x *= x;
            b >>= 1; 
        }
        return res;
    }
}

有限状态自动机

有限状态自动机，就是一种用来进行对象行为建模的工具，其作用主要是描述对象在它的生命周期内所经历的状态序列，以及如何响应来自外界的各种事件，简单来说，就是把他具体抽象为有限个状态，在状态之间进行转化

剑指 Offer 20. 表示数值的字符串 - 力扣（Leetcode）

题意： 给定一个字符串，判断这个字符串是不是代表一个数字，这个数字可能有e ,±,还有小数点等

思路：使用上述所说的有限状态自动机，具体定义了九种状态，画出状态转移图，这是最难的部分

参考题解：剑指 Offer 20. 表示数值的字符串题解

状态的定义：

按照字符串从左到右的顺序，定义以下 9 种状态。

• 开始的空格
• 幂符号前的正负号
• 小数点前的数字
• 小数点、小数点后的数字
• 当小数点前为空格时，小数点、小数点后的数字
• 幂符号
• 幂符号后的正负号
• 幂符号后的数字
• 结尾的空格

class Solution {
    //有限状态机解题
    public boolean isNumber(String s) {
        Map[] states = {
            //在new的时候初始化数据，这里需要两层括号
            new HashMap<>(){{ put(' ', 0);put('s', 1);put('d', 2);put('.', 4); }},
            new HashMap<>(){{ put('d',2);put('.', 4); }},
            new HashMap<>(){{ put('d', 2);put('.', 3);put('e',5);put(' ', 8); }},
            new HashMap<>() {{ put('d', 3); put('e', 5); put(' ', 8); }},              
            new HashMap<>() {{ put('d', 3); }},                                        
            new HashMap<>() {{ put('s', 6); put('d', 7); }},                        
            new HashMap<>() {{ put('d', 7); }},                                        
            new HashMap<>() {{ put('d', 7); put(' ', 8); }},                           
            new HashMap<>() {{ put(' ', 8); }}  
        };
        int p = 0;
        char t;
        for(char c : s.toCharArray()){
            if(c >= '0' && c <= '9') t = 'd';
            else if(c == '+' || c == '-') t = 's';
            else if(c == 'e' || c == 'E') t = 'e';
            else if(c == '.' || c == ' ') t = c;//直接使用符号充当状态机转移的命令
            else t = '?';
            if(!states[p].containsKey(t))  return false; //没有下一个状态
            p = (int)states[p].get(t);//到达下一个状态
        }
        return p == 2 || p == 3 || p == 7 || p == 8;
    }
}

上面的方法不容易想出来，还是来看看if-else吧

if-else大法

class Solution {
    public boolean isNumber(String s) {
        int x = 0,y = s.length() - 1;
        for(int i = 0;i <= y;i++){
            if(s.charAt(i) != ' '){
                x = i;
                break;
            }
        }
        for(int i = y;i >= 0;i--){
            if(s.charAt(i) != ' '){
                y = i;
                break;
            }
        }
        s = s.substring(x,y+1);
        if(s.charAt(0) == '-' || s.charAt(0) == '+'){
            if(s.length() == 1){
                return false;
            }else{
                s = s.substring(1,s.length());
            }
        }
        int flag = 0;
        int note = 0;
        int num = 0;
        
        for(int i = 0;i < s.length();i++){
            if(s.charAt(i) - '0' < 0 || s.charAt(i) > '9'){
                if(s.charAt(i) == 'e' || s.charAt(i) == 'E'){
                    if(num == 1 || i == s.length() - 1 
                    || i == 0){
                        flag = -1;
                    }
                        num = 1;
                }else if(s.charAt(i) == '+' || s.charAt(i) == '-'){
                    if(i==0 || i==s.length()-1||(s.charAt(i-1)!='e'&&s.charAt(i-1)!='E')){
                        System.out.println(i);
                        flag = -1;
                    }
                }
                else if(s.charAt(i) == '.'){
                    if(note == -1){
                        flag = -1;
                    }else if(num!= 1){
                        note = -1;
                    }else{
                        flag = -1;
                    }
                    if((i < s.length() -1 && (s.charAt(i+1)!='e'&&s.charAt(i+1)!='E')) || (i > 0 && (s.charAt(i-1) != 'e'&&s.charAt(i-1) != 'E'))){
                       
                    }else{
                         flag = -1;
                    }

                        if(i == s.length() -1&&i == 0){
                            flag = -1;
                        }
                    
                }else flag = -1;
            }
            if(flag == -1){
                return false;
            }
        }
        
        return true;
    }
}